题目内容
19.一个物体在距地面1m处以初速度4m/s竖直向上抛出,忽略空气阻力.求:(1)物体落地时的速度.(g=10m/s2)
(2)物体到何处时,物体动能与势能相等.
分析 (1)物体做竖直上抛运动,可以看作加速度为-g的匀减速直线运动,由位移速度公式求出落地时的速度;
(2)不计空气阻力,物体的机械能守恒,即可列式,结合条件:重力势能等于动能,可求出高度.
解答 解:(1)设物体的位移为H=-1m,则有
v2$-{v}_{0}^{2}$=-2gH,得 v=$\sqrt{{v}_{0}^{2}-2gh}$=$\sqrt{{4}^{2}-2×10×(-1)}$=6m/s
(2)设在抛出点上方h高处,它的重力势能等于动能,根据机械能守恒定律得
$\frac{1}{2}$mv02+mgh1=mgh+$\frac{1}{2}$mv2
又 mgh=$\frac{1}{2}$mv2
联立得 $\frac{1}{2}$mv${\;}_{0}^{2}$+mgh1=2mgh
解得 h=0.9m
答:
(1)物体落地时的速度为6m/s;
(2)物体到0.9m时,物体动能与势能相等.
点评 竖直上抛运动是常见的运动,是高考的热点,将竖直上抛运动看成一种匀减速直线运动,这样处理比较简单.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
10.有一弹簧振子,振幅为0.8cm,周期为0.5s,初始时具有正方向的最大位移,则它的振动方程是( )
| A. | x=8×10-3sin(4πt+$\frac{π}{2}$)m | B. | x=8×10-3sin(4πt-$\frac{π}{2}$)m | ||
| C. | x=8×10-1sin(πt+$\frac{3π}{2}$)m | D. | x=8×10-1sin($\frac{π}{4}$t+$\frac{π}{2}$)m |
7. 如图所示,两端开口、内径均匀的玻璃弯管竖直固定,两段水银柱将空气柱B封闭在玻璃管左侧的竖直部分,A侧水银有一部分在水平管中.若保持温度不变,向右管缓缓注入少量水银,稳定后( )
如图所示,两端开口、内径均匀的玻璃弯管竖直固定,两段水银柱将空气柱B封闭在玻璃管左侧的竖直部分,A侧水银有一部分在水平管中.若保持温度不变,向右管缓缓注入少量水银,稳定后( )
 如图所示,两端开口、内径均匀的玻璃弯管竖直固定,两段水银柱将空气柱B封闭在玻璃管左侧的竖直部分,A侧水银有一部分在水平管中.若保持温度不变,向右管缓缓注入少量水银,稳定后( )
如图所示,两端开口、内径均匀的玻璃弯管竖直固定,两段水银柱将空气柱B封闭在玻璃管左侧的竖直部分,A侧水银有一部分在水平管中.若保持温度不变,向右管缓缓注入少量水银,稳定后( )| A. | 右侧水银面高度差h1减小 | B. | 空气柱B的长度不变 | ||
| C. | 空气柱B的压强减小 | D. | 左侧水银面高度差h2增大 |
4.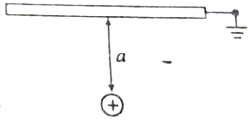 如图所示,在干燥的空气中,质量为m的带正电的点电荷的上面有很大的接地金属板,金属板与点电荷的距离为a,点电荷处于静止状态,真空中静电力常量为k,当地重力加速为g,则点电荷所带的电荷量( )
如图所示,在干燥的空气中,质量为m的带正电的点电荷的上面有很大的接地金属板,金属板与点电荷的距离为a,点电荷处于静止状态,真空中静电力常量为k,当地重力加速为g,则点电荷所带的电荷量( )
 如图所示,在干燥的空气中,质量为m的带正电的点电荷的上面有很大的接地金属板,金属板与点电荷的距离为a,点电荷处于静止状态,真空中静电力常量为k,当地重力加速为g,则点电荷所带的电荷量( )
如图所示,在干燥的空气中,质量为m的带正电的点电荷的上面有很大的接地金属板,金属板与点电荷的距离为a,点电荷处于静止状态,真空中静电力常量为k,当地重力加速为g,则点电荷所带的电荷量( )| A. | 2a$\sqrt{\frac{mg}{k}}$ | B. | a$\sqrt{\frac{mg}{k}}$ | C. | 无穷大 | D. | 0 |
8. 如图所示为一个做匀变速曲线运动的质点的轨迹示意图,已知在B点时的速度与加速度相互垂直,则下列说法中正确的是( )
如图所示为一个做匀变速曲线运动的质点的轨迹示意图,已知在B点时的速度与加速度相互垂直,则下列说法中正确的是( )
 如图所示为一个做匀变速曲线运动的质点的轨迹示意图,已知在B点时的速度与加速度相互垂直,则下列说法中正确的是( )
如图所示为一个做匀变速曲线运动的质点的轨迹示意图,已知在B点时的速度与加速度相互垂直,则下列说法中正确的是( )| A. | D点的速率比C点的速率小 | |
| B. | A点的加速度与速度的夹角小于90° | |
| C. | A点的加速度比D点的加速度大 | |
| D. | 从A到D运动的过程中加速度与速度的夹角一直减小 |
 有一种“傻瓜”相机的曝光时间(快门打开到关闭的时间)是固定不变的.为了估测该相机的曝光时间,有位同学提出了下述实验方案:他从墙面上A点的正上方与A相距H=1.5m处,使一个小石子自由落下,在小石子下落通过A点时,立即按动快门,对小石子照相,得到如图所示的照片,由于石子的运动,它在照片上留下一条模糊的径迹CD.已知每块砖的平均厚度是6cm.请从上述信息和照片上选取估算相机曝光时间必要的物理量.用符号表示,如H等,推出计算曝光时间的关系式,并估算出这个“傻瓜”相机的曝光时间.(要求保留一位有效数字)
有一种“傻瓜”相机的曝光时间(快门打开到关闭的时间)是固定不变的.为了估测该相机的曝光时间,有位同学提出了下述实验方案:他从墙面上A点的正上方与A相距H=1.5m处,使一个小石子自由落下,在小石子下落通过A点时,立即按动快门,对小石子照相,得到如图所示的照片,由于石子的运动,它在照片上留下一条模糊的径迹CD.已知每块砖的平均厚度是6cm.请从上述信息和照片上选取估算相机曝光时间必要的物理量.用符号表示,如H等,推出计算曝光时间的关系式,并估算出这个“傻瓜”相机的曝光时间.(要求保留一位有效数字) 如图甲,匝数n=2的金属线圈(电阻不计)围成的面积为20cm2,线圈与R=2Ω的电阻连接,置于竖直向上、均匀分布的磁场中.磁场与线圈平面垂直,磁感应强度为B,B-t关系如图乙,规定感应电流i从a经过R到b的方向为正方向.则下列i-t关系图正确的是( )
如图甲,匝数n=2的金属线圈(电阻不计)围成的面积为20cm2,线圈与R=2Ω的电阻连接,置于竖直向上、均匀分布的磁场中.磁场与线圈平面垂直,磁感应强度为B,B-t关系如图乙,规定感应电流i从a经过R到b的方向为正方向.则下列i-t关系图正确的是( )


