题目内容
6.某一卫星在赤道上空飞行的,轨道半径为r(小于同步卫星的轨道半径),飞行方向与地球的自转方向相同.设地球的自转角速度为ω0,地球半径为R,地球表面重力加速度为g,在某时刻该卫星通过赤道上某建筑物的上方,则到它下次通过该建筑上方所需时间为( )| A. | 2π$\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$ | B. | 2π($\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$+$\frac{1}{{ω}_{0}}$) | C. | $\frac{2π}{({ω}_{0}-\sqrt{\frac{g{R}^{2}}{{r}^{3}}})}$ | D. | $\frac{2π}{(\sqrt{\frac{g{R}^{2}}{{r}^{3}}}-{ω}_{0})}$ |
分析 根据人造卫星的万有引力等于向心力,列式求出角速度的表达式,卫星再次经过某建筑物的上空,地球多转动一圈.
解答 解:人造卫星绕地球做匀速圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=mω2r,
解得:ω=$\sqrt{\frac{GM}{{r}^{3}}}$…①
卫星再次经过某建筑物的上空,卫星多转动一圈,有:
(ω-ω0)t=2π…②
地球表面的物体受到的重力等于万有引力,即:G$\frac{Mm}{{R}^{2}}$=mg…③
解得:t=$\frac{2π}{\sqrt{\frac{g{R}^{2}}{{r}^{3}}}-{ω}_{0}}$,故ABC错误,正确D.
故选:D.
点评 本题关键:(1)根据万有引力提供向心力求解出角速度;(2)根据地球表面重力等于万有引力得到重力加速度表达式;(3)根据多转动一圈后再次到达某建筑物上空列式.

练习册系列答案
相关题目
16. 如图所示,半径为L的圆管轨道(圆管内径远小于轨道半径)竖直放置,管内壁光滑,管内有一个小球(小球直径略小于管内径)可沿管转动,设小球经过最高点P时的速度为v,则( )
如图所示,半径为L的圆管轨道(圆管内径远小于轨道半径)竖直放置,管内壁光滑,管内有一个小球(小球直径略小于管内径)可沿管转动,设小球经过最高点P时的速度为v,则( )
 如图所示,半径为L的圆管轨道(圆管内径远小于轨道半径)竖直放置,管内壁光滑,管内有一个小球(小球直径略小于管内径)可沿管转动,设小球经过最高点P时的速度为v,则( )
如图所示,半径为L的圆管轨道(圆管内径远小于轨道半径)竖直放置,管内壁光滑,管内有一个小球(小球直径略小于管内径)可沿管转动,设小球经过最高点P时的速度为v,则( )| A. | v的最小值为 $\sqrt{gL}$ | |
| B. | v若增大,球所需的向心力减小 | |
| C. | 当v由$\sqrt{gL}$逐渐减小时,轨道对球的弹力也减小 | |
| D. | 当v由$\sqrt{gL}$逐渐增大时,轨道对球的弹力也增大 |
11.关于力和重力下列说法正确的是( )
| A. | 力可以脱离物体而存在 | |
| B. | 自由下落的石块速度越来越大,说明石块所受重力越来越大 | |
| C. | 物体的重心就是重力的等效作用点 | |
| D. | 物体只有重心这一点才会受到重力作用 |
18.伟大的物理学家伽利略探究物体下落规律的研究方法对于后来的科学研究具有重大的启蒙作用,至今仍然具有重要意义.请你回顾伽利略探究物体下落规律的过程,把下面的重要探究过程按顺序排列正确的是( )
①实验验证 ②遇到问题 ③数学推理 ④提出猜想 ⑤合理外推 ⑥得出结论.
①实验验证 ②遇到问题 ③数学推理 ④提出猜想 ⑤合理外推 ⑥得出结论.
| A. | ②④①⑤③⑥ | B. | ②④①③⑥⑤ | C. | ②④③①⑤⑥ | D. | ②①④③⑥⑤ |
15.质量为m的物块在竖直向上的恒定拉力作用下以加速度a=$\frac{g}{2}$向上加速运动,已知重力加速度为g,空气阻力忽略不计,物块向上运动距离为h的过程,下列说法正确的是( )
| A. | 拉力大小为$\frac{1}{2}$mg | B. | 重力势能增加$\frac{1}{2}$mgh | ||
| C. | 动能增加$\frac{1}{2}$mgh | D. | 机械能增加$\frac{3}{2}$mgh |
16.真空中两个相同的带等量同种电荷的金属小球A和B(均可看作点电荷),分别固定在两处,两球间静电力为F.现用一个不带电与A和B相同的金属小球C先与A接触,再与B接触,然后移开C,再使A、B间距离增大为原来两倍,则A、B两球间的静电力( )
| A. | 表现为引力且是$\frac{F}{8}$ | B. | 表现为斥力且是$\frac{F}{32}$ | ||
| C. | 表现为斥力且是$\frac{3F}{32}$ | D. | 表现为斥力且是$\frac{F}{8}$ |
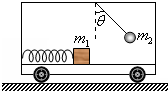 在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k,在车厢的顶部用一根细线悬挂一质量为m2的小球,某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢保持相对静止,如图所示,不计木块与车厢底部的摩擦力,则在这段时间内弹簧的形变为?(说明弹簧是被压缩还是拉长)
在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k,在车厢的顶部用一根细线悬挂一质量为m2的小球,某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢保持相对静止,如图所示,不计木块与车厢底部的摩擦力,则在这段时间内弹簧的形变为?(说明弹簧是被压缩还是拉长)