题目内容
19. 如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )| A. | 小球落地点离O点的水平距离为2R | |
| B. | 小球落地点离O点的水平距离为R | |
| C. | 小球运动到半圆弧最高点P时向心力恰好为零 | |
| D. | 若将半圆弧轨道上部的$\frac{1}{4}$圆弧截去,其他条件不变,则小球能达到的最大高度比P点低 |
分析 小球恰能通过圆弧最高点P,重力恰好提供向心力,可由牛顿第二定律先求出小球通过最高点P的速度,小球离开最高点后做平抛运动,可由动能定理求解落地速度,将半圆弧轨道上部的$\frac{1}{4}$圆弧截去,同样可以用动能定理求解最大高度.
解答 解:AC、小球恰好通过最高点P,在P点,由重力恰好提供向心力,向心力不为零,则有:
mg=m$\frac{{v}_{P}^{2}}{R}$,
解得:vP=$\sqrt{gR}$
小球离开最高点后做平抛运动,则有:
2R=$\frac{1}{2}$gt2
x=vt
解得小球落地点离O点的水平距离为:x=2R,故A正确,BC错误;
D、根据机械能守恒定律可知,小球通过O点的动能等于小球落地点时的动能.
若将半圆弧轨道上部的$\frac{1}{4}$圆弧截去,小球到达最高点时的速度为零,从O到最高点的过程,由动能定理得:
-mg(R+h)=0-Ek
解得:h=1.5R,所以小球能达到的最大高度比P点高1.5R-R=0.5R,故D错误;
故选:A.
点评 本题关键分析清楚物体的运动过程,然后结合平抛运动和动能定理的相关知识进行研究.要注意小球运动过程中,只有重力做功,机械能是守恒的,也要灵活运用.

练习册系列答案
相关题目
9. 某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )
某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )
 某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )
某同学对四个电阻各进行了一次测量,把每个电阻两端的电压和通过它的电流在U-I坐标系中描点,如图所示的a、b、c、d所示( )| A. | a的电阻大于d的电阻 | B. | b的电阻大于c的电阻 | ||
| C. | c的电阻大于d的电阻 | D. | d的电阻大于a的电阻 |
14. 在真空中有两个等量的正电荷q1和q2,分别固定于A、B两点,DC为AB连线的中垂线,C为A、B两点连线的中点,将一正电荷q3由C点沿着中垂线移至无穷远处的过程中,下列结论正确的有( )
在真空中有两个等量的正电荷q1和q2,分别固定于A、B两点,DC为AB连线的中垂线,C为A、B两点连线的中点,将一正电荷q3由C点沿着中垂线移至无穷远处的过程中,下列结论正确的有( )
 在真空中有两个等量的正电荷q1和q2,分别固定于A、B两点,DC为AB连线的中垂线,C为A、B两点连线的中点,将一正电荷q3由C点沿着中垂线移至无穷远处的过程中,下列结论正确的有( )
在真空中有两个等量的正电荷q1和q2,分别固定于A、B两点,DC为AB连线的中垂线,C为A、B两点连线的中点,将一正电荷q3由C点沿着中垂线移至无穷远处的过程中,下列结论正确的有( )| A. | 电势能逐渐减小 | B. | 电势能逐渐增大 | ||
| C. | q3受到的电场力逐渐减小 | D. | q3受到的电场力逐渐增大 |
4. 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度h=$\frac{d}{2}$ | |
| B. | 小环在B处的速度时,环的速度为$\sqrt{(3-2\sqrt{2})gd}$ | |
| C. | 环从A到B,环减少的机械能等于重物增加的机械能 | |
| D. | 环能下降的最大高度为$\frac{4d}{3}$ |
11.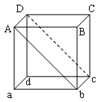 如图所示,把一边长为L的匀质立方体,绕bc棱翻倒,当AbcD平面处于竖直位置时,它的重心位置升高了( )
如图所示,把一边长为L的匀质立方体,绕bc棱翻倒,当AbcD平面处于竖直位置时,它的重心位置升高了( )
 如图所示,把一边长为L的匀质立方体,绕bc棱翻倒,当AbcD平面处于竖直位置时,它的重心位置升高了( )
如图所示,把一边长为L的匀质立方体,绕bc棱翻倒,当AbcD平面处于竖直位置时,它的重心位置升高了( )| A. | $\frac{L}{2}$ | B. | $\frac{\sqrt{2}L}{2}$ | C. | $\frac{(2-\sqrt{2})L}{2}$ | D. | 以上答案都不对 |
8.一个做匀变速直线运动的质点,初速度为0.5m/s,第9s内的位移比第5s内的位移多4m,则该质点的加速度、9s末的速度和质点在9s内通过的位移分别是( )
| A. | a=1m/s2,v=9.5m/s,x=45m | B. | a=1m/s2,v=9m/s,x=45m | ||
| C. | a=1m/s2,v=9m/s,x=40.5m | D. | a=0.8m/s2,v=7.7m/s,x=36.9m |
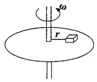 如图所示,有一台水平转盘,盘上有一质量为m 的物体离转轴的距离为r,中间用一根细线相连,物体和转盘之间的动摩擦因数为μ,细线所能承受的最大拉力为3μmg,当圆盘静止时,细线伸直但没有拉力,求:
如图所示,有一台水平转盘,盘上有一质量为m 的物体离转轴的距离为r,中间用一根细线相连,物体和转盘之间的动摩擦因数为μ,细线所能承受的最大拉力为3μmg,当圆盘静止时,细线伸直但没有拉力,求:
 如图是右端开口的圆筒形容器,底面积为S,活塞可以沿容器壁自由滑动.开始时,活塞把一定质量的理想气体封闭在容器内,活塞与容器底部的距离为L,气体温度为T0,大气压强为p0,若给容器内气体加热,让气体膨胀,活塞缓慢移动到与容器底部距离为2L处,求:
如图是右端开口的圆筒形容器,底面积为S,活塞可以沿容器壁自由滑动.开始时,活塞把一定质量的理想气体封闭在容器内,活塞与容器底部的距离为L,气体温度为T0,大气压强为p0,若给容器内气体加热,让气体膨胀,活塞缓慢移动到与容器底部距离为2L处,求: