题目内容
10.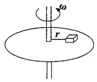 如图所示,有一台水平转盘,盘上有一质量为m 的物体离转轴的距离为r,中间用一根细线相连,物体和转盘之间的动摩擦因数为μ,细线所能承受的最大拉力为3μmg,当圆盘静止时,细线伸直但没有拉力,求:
如图所示,有一台水平转盘,盘上有一质量为m 的物体离转轴的距离为r,中间用一根细线相连,物体和转盘之间的动摩擦因数为μ,细线所能承受的最大拉力为3μmg,当圆盘静止时,细线伸直但没有拉力,求:(1)当圆盘角速度θ1=$\sqrt{\frac{μg}{2r}}$时,细线拉力F1为多大?
(2)当圆盘角速度${θ}_{2}=\sqrt{\frac{3μg}{2r}}$时,细线拉力F2为多大?
(3)圆盘转动的角速度多大时,细线被拉断?
分析 (1)(2)当向心力大于最大静摩擦力时,才会拉紧绳子,先求解只由静摩擦力提供向心力时的临界角速度,判断绳子是否有张力;
(3)绳子的最大拉力和最大静摩擦力的合力提供向心力,根据牛顿第二定律列式求解最大角速度
解答 解:(1)当物体只由静摩擦力提供向心力时,最大的向心力为μmg,此时
μmg≥mω2r
解得:ω≤$\sqrt{\frac{μg}{r}}$
当角速度${ω}_{1}=\sqrt{\frac{μg}{2r}}$时,由于ω1<$\sqrt{\frac{μg}{r}}$,所以细绳拉力T1=0.
(2)当角速度ω2=$\sqrt{\frac{3μg}{2r}}$时,${T}_{2}+μmg={mω}_{2}^{2}r$
所以:${T}_{2}={mω}_{2}^{2}r-μmg$
(3)当拉力达到最大时,转盘有最大角速度ωmax
${T}_{3}+μmg={mω}_{m}^{2}r$
即:3μmg+μmg=m${mω}_{m}^{2}r$
解得:ωm=$\sqrt{\frac{4μg}{r}}$=2$\sqrt{\frac{μg}{r}}$
答:(1)当角速度为ω1=$\sqrt{\frac{μg}{2r}}$时,细绳的拉力是0;
(2)当角速度ω2=$\sqrt{\frac{3μg}{2r}}$时,细绳的拉力是0.5μmg;
(3)转盘转动的最大角速度是$2\sqrt{\frac{μg}{r}}$
点评 本题关键是找到向心力来源,注意当最大静摩擦力不足提供向心力时,绳子才被拉长,发生微小形变,产生弹力

练习册系列答案
相关题目
9.小球由地面竖直上抛,上升的最大高度为H,设所受阻力大小恒定,取地面为零重力势能参考面.在上升至离地高度h处,小球的动能是势能的3倍,在下落至离地高度h处,小球的势能是动能的3倍,则h等于( )
| A. | $\frac{H}{8}$ | B. | $\frac{3H}{8}$ | C. | $\frac{3H}{9}$ | D. | $\frac{4H}{9}$ |
5.一小球以初速度为v0在水平面上做匀减速直线运动,第1s内通过的位移为x1=3m,第2s内通过的位移为x2=2m,从第2秒末开始,小球的速度减小为0时还要运动的位移为x,则下列说法中正确的是( )
| A. | 初速度v0的大小为3.0m/s | B. | 加速度a的大小为1m/s2 | ||
| C. | 位移x的大小为$\frac{9}{8}$m | D. | 位移x内的平均速度大小为0.75m/s |
15.在物理学发展的过程中,关于科学家和他们的贡献,下列说法正确的是( )
| A. | 牛顿提出了万有引力定律,并测定了引力常量G | |
| B. | 伽利略认为力不是维持物体运动的原因,并通过“理想斜面实验”证实了这一说法 | |
| C. | 库仑提出了库仑定律,并最早实验测得元电荷e的数值 | |
| D. | 法拉第根据小磁针在通电导线周围的偏转而发现了电流的磁效应 |
2.关于磁感应强度B=$\frac{F}{IL}$,下列说法正确的是( )
| A. | 电流元IL在磁场中受力为F,则磁感应强度B一定等于$\frac{F}{IL}$ | |
| B. | 磁感应强度大小与电流元IL的乘积成反比,与F成正比 | |
| C. | 磁感应强度方向与电流元IL在此点的受力方向相同 | |
| D. | 以上说法都不对 |
19. 如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
 如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )| A. | 小球落地点离O点的水平距离为2R | |
| B. | 小球落地点离O点的水平距离为R | |
| C. | 小球运动到半圆弧最高点P时向心力恰好为零 | |
| D. | 若将半圆弧轨道上部的$\frac{1}{4}$圆弧截去,其他条件不变,则小球能达到的最大高度比P点低 |
20.从静止开始做匀加速直线运动的物体,前20s内的位移是10m,则该物体运动1min时的位移为( )
| A. | 36 m | B. | 60 m | C. | 90 m | D. | 360 m |
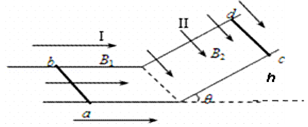 如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2.
如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2. 如图所示,固定在水平面上倾角为α=370、长为s=4.8m的斜面,一个质量为2kg的小物块(可视为质点)放置在斜面上,小物块与斜面间的动摩擦因数μ=0.5,现用大小为F=24N、方向与斜面平行的力推物块,使小物块从斜面的最底端由静止开始向上运动.(sin37°=0.60,cos37°=0.80,g=10m/s2).
如图所示,固定在水平面上倾角为α=370、长为s=4.8m的斜面,一个质量为2kg的小物块(可视为质点)放置在斜面上,小物块与斜面间的动摩擦因数μ=0.5,现用大小为F=24N、方向与斜面平行的力推物块,使小物块从斜面的最底端由静止开始向上运动.(sin37°=0.60,cos37°=0.80,g=10m/s2).