题目内容
15.如图所示,宽L=2m、足够长的金属导轨MN和M′N′放在倾角为θ=30°的斜面上,在N和N′之间连接一个R=2.0Ω的定值电阻,在AA′处放置一根与导轨垂直、质量m=0.8kg、电阻r=2.0Ω的金属杆,杆和导轨间的动摩擦因数μ=$\frac{{\sqrt{3}}}{4}$,导轨电阻不计,导轨处于磁感应强度B=1.0T、方向垂直于导轨平面的匀强磁场中.用轻绳通过定滑轮将电动小车与杆的中点相连,滑轮与杆之间的连线平行于斜面,开始时小车位于滑轮正下方水平面上的P处(小车可视为质点),滑轮离小车的高度H=4.0m.启动电动小车,使之沿PS方向以v=5.0m/s的速度匀速前进,当杆滑到OO′位置时的加速度a=3.2m/s2,AA′与OO′之间的距离d=1m,求:
(1)该过程中,通过电阻R的电量q;
(2)杆通过OO′时的速度大小;
(3)杆在OO′时,轻绳的拉力大小;
(4)上述过程中,若拉力对杆所做的功为13J,求电阻R上的平均电功率.
分析 (1)由法拉第电磁感应定律求出平均感应电动势、由欧姆定律求出平均电流、由电流定义式的变形公式求出通过电阻R的电量q.
(2)由几何关系求出α.根据小车沿绳子方向的分速度等于杆的速度,求杆通过OO′时的速度大小.
(3)由感应电动势为E=BLv,由欧姆定律求出电流,由安培力公式求出安培力,然后由平衡条件求出拉力的大小.
(4)根据动能定理求出克服安培力做功,从而求得电路产生总的电热,由电路的连接关系求出电阻R上产生的电热,即可求解电阻R上的平均电功率.
解答 解:(1)平均感应电动势 $\overline{E}=\frac{△Φ}{△t}=\frac{BLd}{△t}$
通过电阻R的电量 $q=\bar I•△t=\frac{△Φ}{R+r}=\frac{BLd}{R+r}$
代入数据,可得:q=0.5C
(2)几何关系:$\frac{H}{sinα}-H=d$
解得:sinα=0.8,α=53°
杆的速度等于小车速度沿绳方向的分量:v1=vcosα=5×0.6=3m/s
(3)杆受的摩擦力 Ff=μmgcosθ=$\frac{\sqrt{3}}{4}$×0.8×10×$\frac{\sqrt{3}}{2}$=3N
杆受的安培力${F_安}=BIL=\frac{{{B^2}{L^2}{{v}_1}}}{(R+r)}$
代入数据,可得 F安=3N
根据牛顿第二定律:FT-mgsinθ-Ff-F安=ma
解得:FT=12.56N
(4)根据动能定理:$W+{W_安}-mgdsinθ-{F_f}=\frac{1}{2}mv_1^2$
解出 W安=-2.4J
则电路产生总的电热 Q总=2.4J
由于R=r,那么,R上的电热 QR=1.2J
此过程所用的时间 t=$\frac{Hcotα}{v}$=$\frac{4×cot53°}{5}$s=0.6s
R上的平均电功率 $\overline{P}=\frac{Q_R}{t}=\frac{1.2}{0.6}W=2.0W$
答:
(1)该过程中,通过电阻R的电量q是0.5C;
(2)杆通过OO′时的速度大小是3m/s;
(3)杆在OO′时,轻绳的拉力大小是12.56N;
(4)电阻R上的平均电功率是2.0W.
点评 本题是一道电磁感应与力学、电学相结合的综合题,分析清楚滑杆的运动过程,应用运动的合成与分解分析小车与杆的速度关系是关键.运用E=BLv、欧姆定律、安培力公式、牛顿第二定律、平衡条件、能量守恒定律即可正确解题;求R产生的热量时要注意,系统产生的总热量是R与r产生的热量之和.

| A. | 力可以没有施力物体,但不能离开受力物体 | |
| B. | 物体各部分都受到重力,可将物体的重力等效集中在一点,这一点叫物体的重心 | |
| C. | 自然界只有三种基本相互作用,分别是电磁相互作用、强相互作用、弱相互作用 | |
| D. | 只有直接接触的物体间才有力 |
 如图所示,虚线框内为某种电磁缓冲车的结构示意图,其主要部件为缓冲滑块K和质量为m的缓冲车厢.在缓冲车厢的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN,缓冲车厢的底部安装电磁铁(未画出,其中m含电磁铁的质量>,能产生垂直于导轨平面向下的匀强磁场,磁场的磁感应强度大小为B,导轨内的缓冲滑块K由高强度绝缘材料制成,滑块K上绕有闭合矩形线圈abcd,线圈的总电阻为R、匣数为n,ab边长为L,假设缓冲车厢以速度v0与障碍物C碰撞后,滑块K立即停下,而缓冲车厢继续向前移动距离L后速度为零,已知缓冲车厢与障碍物、缓冲车厢与线圈的ab边均没有接触,不计一切摩擦阻力,在这个缓冲过程中,下列说法正确的是( )
如图所示,虚线框内为某种电磁缓冲车的结构示意图,其主要部件为缓冲滑块K和质量为m的缓冲车厢.在缓冲车厢的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN,缓冲车厢的底部安装电磁铁(未画出,其中m含电磁铁的质量>,能产生垂直于导轨平面向下的匀强磁场,磁场的磁感应强度大小为B,导轨内的缓冲滑块K由高强度绝缘材料制成,滑块K上绕有闭合矩形线圈abcd,线圈的总电阻为R、匣数为n,ab边长为L,假设缓冲车厢以速度v0与障碍物C碰撞后,滑块K立即停下,而缓冲车厢继续向前移动距离L后速度为零,已知缓冲车厢与障碍物、缓冲车厢与线圈的ab边均没有接触,不计一切摩擦阻力,在这个缓冲过程中,下列说法正确的是( )| A. | 线圈中的感应电流沿顺时针方向(俯视〕,且最大感应电流为$\frac{nBL{v}_{0}}{R}$ | |
| B. | 缓冲滑块K受到的磁场作用力使缓冲车厢减速运动,从而实现缓冲 | |
| C. | 此过程中,通过线圈abcd的电荷量为$\frac{nB{L}^{2}}{R}$ | |
| D. | 此过程中,线圈abcd产生的焦耳热为$\frac{m{v}_{0}^{2}}{2}$ |
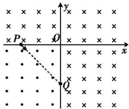 如图所示,在xOy平面内存在磁感应强度大小为B的匀强磁场,第一、二、四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外.P(-L,0)、Q(0,-L)为坐标轴上的两个点.现有一电子从P点沿PQ方向射出,不计电子的重力,下列说法正确的是( )
如图所示,在xOy平面内存在磁感应强度大小为B的匀强磁场,第一、二、四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外.P(-L,0)、Q(0,-L)为坐标轴上的两个点.现有一电子从P点沿PQ方向射出,不计电子的重力,下列说法正确的是( )| A. | 若电子从P点出发恰好经原点O第一次射出磁场分界线,则电子运动的路程一定为$\frac{πL}{2}$ | |
| B. | 若电子从P点出发经原点O到达Q点,则电子运动的路程一定为πL | |
| C. | 若电子从P点出发经原点O到达Q点,则电子运动的路程一定为2πL | |
| D. | 若电子从P点出发经原点O到达Q点,则电子运动的路程可能为πL,也可能为2πL |
 如图,正方形容器处在匀强磁场中,一束电子从孔a垂直于磁场沿ab方向射入容器中,其中一部分从c孔射出,一部分从d孔射出,容器处在真空中,下列说法正确的是( )
如图,正方形容器处在匀强磁场中,一束电子从孔a垂直于磁场沿ab方向射入容器中,其中一部分从c孔射出,一部分从d孔射出,容器处在真空中,下列说法正确的是( )| A. | 从两孔射出的电子速率之比为vc:vd=2:1 | |
| B. | 从两孔射出的电子在容器中运动的时间之比tc:td=1:2 | |
| C. | 从两孔射出的电子的加速度大小之比ac:ad=$\sqrt{2}$:1 | |
| D. | 从两孔射出的电子的加速度大小之比ac:ad=2:1 |
 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距离L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆ab,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆ab,使之由静止开始运动,最终以8m/s的速度做匀速直线运动.若此时闭合开关S,释放的α粒子经加速电场C加速从d孔对着圆心O进入半径r=$\sqrt{3}m$的固定圆筒中(筒壁上的小孔d只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为B2的匀强磁场,α粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失.(α粒子质量m≈6.4×10-27kg,电荷量q=3.2×10-19C).求:
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距离L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆ab,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆ab,使之由静止开始运动,最终以8m/s的速度做匀速直线运动.若此时闭合开关S,释放的α粒子经加速电场C加速从d孔对着圆心O进入半径r=$\sqrt{3}m$的固定圆筒中(筒壁上的小孔d只能容一个粒子通过),圆筒内有垂直水平面向下的磁感应强度为B2的匀强磁场,α粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失.(α粒子质量m≈6.4×10-27kg,电荷量q=3.2×10-19C).求: 如图,竖直平面内放着两根间距L=1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R=2Ω的电阻,N板上有一小孔Q,在金属板M、N之间CD上方有垂直纸面向里的磁感应强度B0=1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T.有一质量M=0.2kg、电阻r=1Ω的金属棒搭在M、N之间并与M、N良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点由静止释放一个比荷$\frac{q}{m}$=1×104 C/kg的正离子,经电场加速后,以v=200m/s的速度从Q点垂直于N板边界射入右侧区域.不计离子重力,忽略电流产生的磁场,取g=10m/s2.求:
如图,竖直平面内放着两根间距L=1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R=2Ω的电阻,N板上有一小孔Q,在金属板M、N之间CD上方有垂直纸面向里的磁感应强度B0=1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T.有一质量M=0.2kg、电阻r=1Ω的金属棒搭在M、N之间并与M、N良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点由静止释放一个比荷$\frac{q}{m}$=1×104 C/kg的正离子,经电场加速后,以v=200m/s的速度从Q点垂直于N板边界射入右侧区域.不计离子重力,忽略电流产生的磁场,取g=10m/s2.求: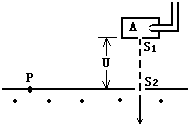 如图所示为测量某种离子的比荷的装置,让中性气体分子进入电离室A,在那里被电离成离子.这些离子从电离室的小孔飘出,从缝S1进入加速电场被加速,然后让离子从缝S2垂直进入匀强磁场,最后打在底片上的P点.已知加速电压为U,磁场的磁感应强度为B,缝S2与P之间的距离为a,离子从缝S1进入电场时的速度不计,求:
如图所示为测量某种离子的比荷的装置,让中性气体分子进入电离室A,在那里被电离成离子.这些离子从电离室的小孔飘出,从缝S1进入加速电场被加速,然后让离子从缝S2垂直进入匀强磁场,最后打在底片上的P点.已知加速电压为U,磁场的磁感应强度为B,缝S2与P之间的距离为a,离子从缝S1进入电场时的速度不计,求: 固定在匀强磁场中的正方形导线框abcd,各边长为L,其中ab是一段电阻为R的均匀电阻丝,其余三边均为电阻可以忽略的铜线,磁感应强度为B的匀强磁场方向垂直纸面向里.现有一段与ab材料、粗细、长度均相同的电阻丝PQ架在导线框上,如图所示.若PQ以恒定速度v从ad滑向bc,当其滑过$\frac{L}{3}$的距离时,通过Pb段的电流多大?方向如何?
固定在匀强磁场中的正方形导线框abcd,各边长为L,其中ab是一段电阻为R的均匀电阻丝,其余三边均为电阻可以忽略的铜线,磁感应强度为B的匀强磁场方向垂直纸面向里.现有一段与ab材料、粗细、长度均相同的电阻丝PQ架在导线框上,如图所示.若PQ以恒定速度v从ad滑向bc,当其滑过$\frac{L}{3}$的距离时,通过Pb段的电流多大?方向如何?