题目内容
2.如图甲所示,在竖直平面内固定一光滑的半圆形轨道ABC,小球以一定的初速度从最低点A冲上轨道,图乙是小球在半圆形轨道上从A运动到C的过程中,其速度平方与其对应高度的关系图象.已知小球在最高点C受到轨道的作用力为1.25N,空气阻力不计,g=10m/s2,B点为AC轨道中点,下列说法正确的是( )
| A. | 小球质量为0.5kg | B. | 小球在B点受到轨道作用力为4.25N | ||
| C. | 图乙中x=25m2/s2 | D. | 小球在A点时重力的功率为5W |
分析 根据机械能守恒可由图乙得到x,然后根据在C点小球受到的合外力,由牛顿第二定律可求得质量,进而得到根据在B点的速度得到受力情况.
解答 解:C、小球在光滑轨道上运动,只有重力做功,故机械能守恒,所以有:
$\frac{1}{2}m{{v}_{A}}^{2}=\frac{1}{2}m{{v}_{h}}^{2}+mgh$;
解得:${{v}_{A}}^{2}={{v}_{h}}^{2}+2gh$
即为:x=9+2×10×0.8m2/s2=25m2/s2,故C正确;
A、由图乙可知,轨道半径R=0.4m,小球在C点的速度vC=3m/s,那么由牛顿第二定律可得:
$F+mg=\frac{m{{v}_{C}}^{2}}{R}$;
解得:$m=\frac{F}{\frac{{{v}_{C}}^{2}}{R}-g}$=$\frac{1.25}{\frac{9}{0.4}-10}kg=0.1kg$,故A错误;
B、由机械能守恒可得在B点的速度为:
${v}_{B}=\sqrt{{{v}_{A}}^{2}-2gR}=\sqrt{25-2×10×0.4}m/s=\sqrt{17}m/s$;
所以,小球在B点受到的在水平方向上的合外力做向心力为:
$F=\frac{m{{v}_{B}}^{2}}{R}=\frac{0.1×17}{0.4}N=4.25N$
所以,小球在B点受到轨道作用力为4.25N,故B正确;
D、小球在A点时重力G=mg=1N,方向向下;速度vA=5m/s,方向向右,故小球在A点时重力的功率为0,故D错误;
故选:BC.
点评 物体运动学问题,一般先对物体进行受力分析,若要求过程量如加速度,则应用牛顿第二定律求解;若要求的时状态量,如速度,则一般应用动能定理求解,

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
13.如图所示,在同一水平面内有两根足够长的光滑水平金属导轨,间距为20$\sqrt{2}$ cm,电阻不计,其左端连接一阻值为10Ω的定值电阻,两导轨之间存在着磁感应强度为1T的匀强磁场,磁场边界虚线由多个正弦曲线的半周期衔接而成,磁场方向如图,一接入电阻阻值为10Ω的导体棒AB在外力作用下以10m/s的速度匀速向右运动,交流电压表和交流电流表均为理想电表,则( )
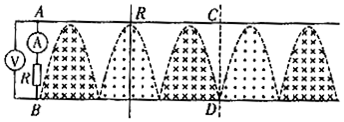

| A. | 电流表的示数是$\frac{\sqrt{2}}{10}$ A | |
| B. | 电压表的示数是1V | |
| C. | 导体棒运动到图示虚线CD位置时,电流表示数为零 | |
| D. | 导体棒上消耗的热功率为0.1W |
10. 竖直平面内有一金属环,半径为a,总电阻为R,超感应强度为B的匀强磁场垂直穿过半个金属环平面(如图所示),与环的最高点A铰链连接的长度为2a,电阻为$\frac{R}{2}$的导体棒AB由水平位置紧贴环面摆下,当摆到竖直位置时,B点的线速度为v,则这时AB两端的电压大小为( )
竖直平面内有一金属环,半径为a,总电阻为R,超感应强度为B的匀强磁场垂直穿过半个金属环平面(如图所示),与环的最高点A铰链连接的长度为2a,电阻为$\frac{R}{2}$的导体棒AB由水平位置紧贴环面摆下,当摆到竖直位置时,B点的线速度为v,则这时AB两端的电压大小为( )
 竖直平面内有一金属环,半径为a,总电阻为R,超感应强度为B的匀强磁场垂直穿过半个金属环平面(如图所示),与环的最高点A铰链连接的长度为2a,电阻为$\frac{R}{2}$的导体棒AB由水平位置紧贴环面摆下,当摆到竖直位置时,B点的线速度为v,则这时AB两端的电压大小为( )
竖直平面内有一金属环,半径为a,总电阻为R,超感应强度为B的匀强磁场垂直穿过半个金属环平面(如图所示),与环的最高点A铰链连接的长度为2a,电阻为$\frac{R}{2}$的导体棒AB由水平位置紧贴环面摆下,当摆到竖直位置时,B点的线速度为v,则这时AB两端的电压大小为( )| A. | $\frac{Bav}{2}$ | B. | $\frac{3Bav}{8}$ | C. | $\frac{Bav}{4}$ | D. | $\frac{Bav}{3}$ |
17. 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面,有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值相等,与导轨之间的动摩擦因数μ,导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F,此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面,有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值相等,与导轨之间的动摩擦因数μ,导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F,此时( )
 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面,有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值相等,与导轨之间的动摩擦因数μ,导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F,此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面,有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值相等,与导轨之间的动摩擦因数μ,导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F,此时( )| A. | 电阻R2的电热功率为$\frac{Fv}{6}$ | |
| B. | 电阻R1的电热功率为$\frac{Fv}{3}$ | |
| C. | 整个装置消耗的机械功率为Fv | |
| D. | 整个装置因摩擦而产生的热功率为μmgvcosθ |
14. 如图所示,正方形ABCD以坐标原点O为中心,关于x轴对称,与x轴交于M、N两点,带电量均为Q的点电荷固定在正方形的四个顶点,其中A、B处点电荷带正电,C、D处点电荷带负电.下列说法正确的是( )
如图所示,正方形ABCD以坐标原点O为中心,关于x轴对称,与x轴交于M、N两点,带电量均为Q的点电荷固定在正方形的四个顶点,其中A、B处点电荷带正电,C、D处点电荷带负电.下列说法正确的是( )
 如图所示,正方形ABCD以坐标原点O为中心,关于x轴对称,与x轴交于M、N两点,带电量均为Q的点电荷固定在正方形的四个顶点,其中A、B处点电荷带正电,C、D处点电荷带负电.下列说法正确的是( )
如图所示,正方形ABCD以坐标原点O为中心,关于x轴对称,与x轴交于M、N两点,带电量均为Q的点电荷固定在正方形的四个顶点,其中A、B处点电荷带正电,C、D处点电荷带负电.下列说法正确的是( )| A. | M、N两点电场强度等大反向 | |
| B. | 在x轴上从M点到N点,电势先降低后升高 | |
| C. | 在x轴上M点左侧、N点右侧都存在场强为零的点 | |
| D. | 负检验电荷在M点具有的电势能比其在N点的电势能多 |
11.篮球运动员通常伸出双手迎接传来的篮球,接球时两手随球迅速收缩至胸前.这样做的目的是( )
| A. | 增加作用时间,减小球对手的冲量 | |
| B. | 增加作用时间,减小球对手的冲击力 | |
| C. | 减小作用时间,减小球的动量变化量 | |
| D. | 减小作用时间,增加球的动量变化量 |
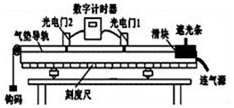 一同学想利用如图所示的气垫导轨实验装置探究动能定理.
一同学想利用如图所示的气垫导轨实验装置探究动能定理. 如图所示,一半径为R,内表面粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平.一质量为m的小球自P点正上方高度R处由静止开始下落,恰好从P点进入轨道.小球滑到轨道最低点N时,对轨道的压力为4mg,重力加速度的大小为g,小球可视为质点,不计空气阻力.
如图所示,一半径为R,内表面粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平.一质量为m的小球自P点正上方高度R处由静止开始下落,恰好从P点进入轨道.小球滑到轨道最低点N时,对轨道的压力为4mg,重力加速度的大小为g,小球可视为质点,不计空气阻力. 如图所示,两金属导轨形成斜面,导轨间距离为d,倾角为37°,MN和PQ间存在垂直于斜面向上的磁场.a、b两导体棒垂直于导轨,两导体棒间距离为d=1m,a导体棒距离磁场上边界MN的距离为d=1m.a导体棒的质量为ma=0.2kg,b导体棒的质量为mb=0.1kg,两导体棒与导轨的动摩擦因数均为μ=0.5,除两导体棒外,其余电阻不计,由静止同时释放a、b两导体棒,当a导体棒进入磁场时恰好做匀速直线运动,当b导体棒刚好进入磁场时,a导体棒正好离开磁场,b导体棒在离开磁场前已经做匀速运动.(sin37°=0.6,cos37°=0.8)
如图所示,两金属导轨形成斜面,导轨间距离为d,倾角为37°,MN和PQ间存在垂直于斜面向上的磁场.a、b两导体棒垂直于导轨,两导体棒间距离为d=1m,a导体棒距离磁场上边界MN的距离为d=1m.a导体棒的质量为ma=0.2kg,b导体棒的质量为mb=0.1kg,两导体棒与导轨的动摩擦因数均为μ=0.5,除两导体棒外,其余电阻不计,由静止同时释放a、b两导体棒,当a导体棒进入磁场时恰好做匀速直线运动,当b导体棒刚好进入磁场时,a导体棒正好离开磁场,b导体棒在离开磁场前已经做匀速运动.(sin37°=0.6,cos37°=0.8)