题目内容
8.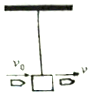 如图所示,用细线挂以质量为M的木块,有一质量为m的子弹自左向右水平射穿此木块,穿透前后子弹的速度分别为vo 和v(设子弹穿过木块的时间和空气阻力不计),求子弹穿出后木块上升的最大高度h.
如图所示,用细线挂以质量为M的木块,有一质量为m的子弹自左向右水平射穿此木块,穿透前后子弹的速度分别为vo 和v(设子弹穿过木块的时间和空气阻力不计),求子弹穿出后木块上升的最大高度h.
分析 由于子弹穿过木块的时间不计,外力的冲量近似为零,子弹和木块组成的系统动量近似守恒,由动量守恒定律求解木块的速度大小.再对木块由机械能守恒可求得上升的高度.
解答 解:根据动量守恒定律得
mv0=mv+Mv′,
对木块由机械能守恒定律可知
Mgh=$\frac{1}{2}$Mv′2;
联立解得:h=$\frac{{m}^{2}({v}_{0}-v)^{2}}{2{M}^{2}g}$
答:弹穿出后木块上升的最大高度h为$\frac{{m}^{2}({v}_{0}-v)^{2}}{2{M}^{2}g}$
点评 子弹打击木块与碰撞过程类似,基本规律是系统的动量守恒.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.肥皂泡呈现的彩色、露珠呈现的彩色、通过狭缝看白光源得到的彩色,它们分别属于( )
| A. | 光的干涉、衍射和色散现象 | B. | 光的衍射、色散和干涉现象 | ||
| C. | 光的干涉、色散和衍射现象 | D. | 光的色散、干涉和衍射现象 |
17.一个小水电站,输出的电功率为20kW,输电线总电阻为0.5Ω,如果先用400V的电压输送,后又改用2 000V的电压输送,则输送电压提高后,输电导线上损失的电功率变化情况是( )
| A. | 减少50 W | B. | 减少1 200 W | C. | 减少7.68×106 W | D. | 增大7.68×106 W |

 如图,水平光滑轨道ab和光滑曲面bd相切于b,轨道最高点d距水平地面高度为h,一质量为m的物块在水平恒力的作用下由静止开始开始从a运动到b后撤去F,物块最后从d点水平抛出,已知ab间距离为L.忽略空气阻力.试求:
如图,水平光滑轨道ab和光滑曲面bd相切于b,轨道最高点d距水平地面高度为h,一质量为m的物块在水平恒力的作用下由静止开始开始从a运动到b后撤去F,物块最后从d点水平抛出,已知ab间距离为L.忽略空气阻力.试求: 如图,S为某一放射源,能源源不断的向水平方向放射出带电粒子流.为了测定该放射源所放射粒子的性质和放射强度,有人设计了如图所示测定装置,在放射源S与极板A之间设置一加速电压U,使放射粒子流经过加速后由P点射入半径为R的圆形区域,区域内有磁感应强度为B的匀强磁场.C为粒子能量接收显示器,可以沿圆形磁场区域边界自由移动.实验中发现,当接收器C移到Q点时,能接收到放射粒子,测得图中粒子的偏转角为θ.不计放射粒子的初速度和重力.
如图,S为某一放射源,能源源不断的向水平方向放射出带电粒子流.为了测定该放射源所放射粒子的性质和放射强度,有人设计了如图所示测定装置,在放射源S与极板A之间设置一加速电压U,使放射粒子流经过加速后由P点射入半径为R的圆形区域,区域内有磁感应强度为B的匀强磁场.C为粒子能量接收显示器,可以沿圆形磁场区域边界自由移动.实验中发现,当接收器C移到Q点时,能接收到放射粒子,测得图中粒子的偏转角为θ.不计放射粒子的初速度和重力. 如图所示,A、B为半径分别是R、2R的同心轮,与半径为R的C轮用皮带传动,且不打滑,a、b、c分别为三轮边缘上的三个点,则这三个点的线速度之比为:2:1:2;这三个点的角速度之比为:1:1:2;这三个点的向心加速度之比为:2:1:4.
如图所示,A、B为半径分别是R、2R的同心轮,与半径为R的C轮用皮带传动,且不打滑,a、b、c分别为三轮边缘上的三个点,则这三个点的线速度之比为:2:1:2;这三个点的角速度之比为:1:1:2;这三个点的向心加速度之比为:2:1:4. 一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,并且波刚好传到x=4m处,再经0.3s时间质点a第一次达到波峰位置,则质点b刚开始振动时的运动方向为沿y轴向上,质点b第一次出现在波峰的时刻为0.5s.
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,并且波刚好传到x=4m处,再经0.3s时间质点a第一次达到波峰位置,则质点b刚开始振动时的运动方向为沿y轴向上,质点b第一次出现在波峰的时刻为0.5s.