题目内容
3. 如图,水平光滑轨道ab和光滑曲面bd相切于b,轨道最高点d距水平地面高度为h,一质量为m的物块在水平恒力的作用下由静止开始开始从a运动到b后撤去F,物块最后从d点水平抛出,已知ab间距离为L.忽略空气阻力.试求:
如图,水平光滑轨道ab和光滑曲面bd相切于b,轨道最高点d距水平地面高度为h,一质量为m的物块在水平恒力的作用下由静止开始开始从a运动到b后撤去F,物块最后从d点水平抛出,已知ab间距离为L.忽略空气阻力.试求:(1)物块从a运动到b所用的时间.
(2)物块到达d点时的速度.
(3)物块从d点到着地的水平距离.
分析 (1)小球从a运动到b的过程中摩擦力做功,可以得出动能定律的方程;由动量定理求时间;
(2)应用机械能守恒求d点的速度.
(3)从d点做平抛运动,根据x=Vt求距离
解答 解:(1)根据动能定理:FL=$\frac{1}{2}m{V}_{b}^{2}$
由动量定理:Ft=mVb
联立得:t=$\sqrt{\frac{2mL}{F}}$
(2)应用机械能守恒:$\frac{1}{2}m{V}_{b}^{2}$=mgh+$\frac{1}{2}m{V}_{d}^{2}$
解得:Vd=$\sqrt{\frac{2(FL-mgh)}{m}}$
(3)从d点做平抛运动,则:Vdt′=X
$t′=\sqrt{\frac{2h}{g}}$
解得:X=$2\sqrt{\frac{h(FL-mgh)}{mg}}$
答:(1)物块从a运动到b所用的时间$\sqrt{\frac{2mL}{F}}$.
(2)物块到达d点时的速度$\sqrt{\frac{2(FL-mgh)}{m}}$.
(3)物块从d点到着地的水平距离$2\sqrt{\frac{h(FL-mgh)}{mg}}$.
点评 本题比较简单,考查了动能定理、机械能守恒定律的应用,应用动能定理时要注意求出所有力做的功,且注意正负.

练习册系列答案
相关题目
18. 如图所示,a、b的质量均为m,a从倾角为450的光滑固定斜面顶端无初速度下滑,b同时从斜面顶端以速度v0水平抛出,对二者运动过程以下说法正确的是( )
如图所示,a、b的质量均为m,a从倾角为450的光滑固定斜面顶端无初速度下滑,b同时从斜面顶端以速度v0水平抛出,对二者运动过程以下说法正确的是( )
 如图所示,a、b的质量均为m,a从倾角为450的光滑固定斜面顶端无初速度下滑,b同时从斜面顶端以速度v0水平抛出,对二者运动过程以下说法正确的是( )
如图所示,a、b的质量均为m,a从倾角为450的光滑固定斜面顶端无初速度下滑,b同时从斜面顶端以速度v0水平抛出,对二者运动过程以下说法正确的是( )| A. | 落地前的瞬间二者速率相同 | B. | 二者加速度始终相同 | ||
| C. | a、b都做匀变速运动 | D. | a、b同时落地 |
15.关于向心力的说法中正确的是( )
| A. | 物体由于做圆周运动而产生了一个指向圆心的力就是向心力 | |
| B. | 向心力不能改变做圆周运动物体的速度大小 | |
| C. | 做匀速圆周运动的物体,其向心力是不变的 | |
| D. | 做圆周运动的物体,其所受外力的合力的方向一定指向圆心 |


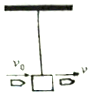 如图所示,用细线挂以质量为M的木块,有一质量为m的子弹自左向右水平射穿此木块,穿透前后子弹的速度分别为vo 和v(设子弹穿过木块的时间和空气阻力不计),求子弹穿出后木块上升的最大高度h.
如图所示,用细线挂以质量为M的木块,有一质量为m的子弹自左向右水平射穿此木块,穿透前后子弹的速度分别为vo 和v(设子弹穿过木块的时间和空气阻力不计),求子弹穿出后木块上升的最大高度h.