题目内容
13. 如图,S为某一放射源,能源源不断的向水平方向放射出带电粒子流.为了测定该放射源所放射粒子的性质和放射强度,有人设计了如图所示测定装置,在放射源S与极板A之间设置一加速电压U,使放射粒子流经过加速后由P点射入半径为R的圆形区域,区域内有磁感应强度为B的匀强磁场.C为粒子能量接收显示器,可以沿圆形磁场区域边界自由移动.实验中发现,当接收器C移到Q点时,能接收到放射粒子,测得图中粒子的偏转角为θ.不计放射粒子的初速度和重力.
如图,S为某一放射源,能源源不断的向水平方向放射出带电粒子流.为了测定该放射源所放射粒子的性质和放射强度,有人设计了如图所示测定装置,在放射源S与极板A之间设置一加速电压U,使放射粒子流经过加速后由P点射入半径为R的圆形区域,区域内有磁感应强度为B的匀强磁场.C为粒子能量接收显示器,可以沿圆形磁场区域边界自由移动.实验中发现,当接收器C移到Q点时,能接收到放射粒子,测得图中粒子的偏转角为θ.不计放射粒子的初速度和重力.(1)根据以上数据,试求该粒子的比荷 $\frac{q}{m}$;
(2)若能量接收显示器C显示每秒接收到的能量为E,则此放射粒子流的等效电流多大?
分析 根据动能定理求出粒子进入磁场时的速度,根据几何关系求出粒子在磁场中的半径,根据半径公式求出粒子的比荷.
等效电流等于单位时间内流过某个横截面的电量,结合电流的定义式进行求解.
解答  解:(1)根据动能定理得,qU=$\frac{1}{2}m{v}^{2}$,
解:(1)根据动能定理得,qU=$\frac{1}{2}m{v}^{2}$,
解得v=$\sqrt{\frac{2qU}{m}}$,
根据几何关系知,粒子在磁场中做匀速圆周运动的半径r=$Rcot\frac{θ}{2}$,
根据qvB=$m\frac{{v}^{2}}{r}$得,r=$\frac{mv}{qB}$,
联立解得$\frac{q}{m}$=$\frac{v}{BRcot\frac{θ}{2}}$.
(2)每个粒子的动能为qU,
则每秒接收粒子的个数n=$\frac{E}{qU}$,
等效电流等于单位时间内流过某个横截面的电量,则I=$\frac{nq}{1}=\frac{E}{U}$.
答:(1)粒子的比荷 $\frac{q}{m}$为$\frac{v}{BRcot\frac{θ}{2}}$.
(2)此放射粒子流的等效电流为$\frac{E}{U}$.
点评 本题考查了带电粒子在电场中的加速和磁场中的偏转,通过几何关系求出粒子在磁场中的半径是解决本题的关键.

练习册系列答案
相关题目
3. 如图,真空中A、B两点相距2r.O点是AB连线的中点,图中虚线是AB连线的中垂线,中垂线上的C点与O点相距r,A、B点分别固定一个的点电荷+QA和-QB.已知两点电荷电量大小相等,+QA在C点形成的电场的场强大小为EA,电势为φA,规定无穷远处电势为0,则关于-QB在C点形成电场的场强和电势的说法正确的是(电势是标量,叠加时不遵从平行四边形定则)( )
如图,真空中A、B两点相距2r.O点是AB连线的中点,图中虚线是AB连线的中垂线,中垂线上的C点与O点相距r,A、B点分别固定一个的点电荷+QA和-QB.已知两点电荷电量大小相等,+QA在C点形成的电场的场强大小为EA,电势为φA,规定无穷远处电势为0,则关于-QB在C点形成电场的场强和电势的说法正确的是(电势是标量,叠加时不遵从平行四边形定则)( )
 如图,真空中A、B两点相距2r.O点是AB连线的中点,图中虚线是AB连线的中垂线,中垂线上的C点与O点相距r,A、B点分别固定一个的点电荷+QA和-QB.已知两点电荷电量大小相等,+QA在C点形成的电场的场强大小为EA,电势为φA,规定无穷远处电势为0,则关于-QB在C点形成电场的场强和电势的说法正确的是(电势是标量,叠加时不遵从平行四边形定则)( )
如图,真空中A、B两点相距2r.O点是AB连线的中点,图中虚线是AB连线的中垂线,中垂线上的C点与O点相距r,A、B点分别固定一个的点电荷+QA和-QB.已知两点电荷电量大小相等,+QA在C点形成的电场的场强大小为EA,电势为φA,规定无穷远处电势为0,则关于-QB在C点形成电场的场强和电势的说法正确的是(电势是标量,叠加时不遵从平行四边形定则)( )| A. | 场强大小为EA,方向与+QA在C点形成的电场方向相同 | |
| B. | 场强大小为EA,方向与+QA在C点形成的电场方向垂直 | |
| C. | 电势为φA | |
| D. | 电势为-φA |
4. 火车轨道在转弯处外轨高于内轨,当列车以V的规定速度行驶时,其做圆周运动的向心力刚好由火车的重力和轨道平面的支持力提供,则以下说法中正确的是( )
火车轨道在转弯处外轨高于内轨,当列车以V的规定速度行驶时,其做圆周运动的向心力刚好由火车的重力和轨道平面的支持力提供,则以下说法中正确的是( )
 火车轨道在转弯处外轨高于内轨,当列车以V的规定速度行驶时,其做圆周运动的向心力刚好由火车的重力和轨道平面的支持力提供,则以下说法中正确的是( )
火车轨道在转弯处外轨高于内轨,当列车以V的规定速度行驶时,其做圆周运动的向心力刚好由火车的重力和轨道平面的支持力提供,则以下说法中正确的是( )| A. | 当火车转弯速度大于V时,内轨对轮缘有挤压 | |
| B. | 当火车转弯速度大于V时,外轨对轮缘有挤压 | |
| C. | 当火车转弯速度小于V时,内轨对轮缘有挤压 | |
| D. | 当火车转弯速度小于V时,外轨对轮缘有挤压 |
5.质量为0.2kg的小球做自由落体运动,在其下落过程中,第1s末重力做功的瞬时功率为 ;1s内重力做功的平均功率为 (g取10m/s2)( )
| A. | 10 W;10 W | B. | 15 W;15 W | C. | 20 W;10 W | D. | 25 W;15 W |
2.汽车通过圆形拱桥顶点时对桥的压力为车重的$\frac{1}{2}$,若拱桥的半径为R=20m,则此时汽车的速度为( )
| A. | 10m/s | B. | 20m/s | C. | 25m/s | D. | 30m/s |
3. 交流电源电压u=20$\sqrt{2}$sin(100 πt)V,电路中电阻R=10Ω.则如图电路中理想电流表和电压表的读数分别为( )
交流电源电压u=20$\sqrt{2}$sin(100 πt)V,电路中电阻R=10Ω.则如图电路中理想电流表和电压表的读数分别为( )
 交流电源电压u=20$\sqrt{2}$sin(100 πt)V,电路中电阻R=10Ω.则如图电路中理想电流表和电压表的读数分别为( )
交流电源电压u=20$\sqrt{2}$sin(100 πt)V,电路中电阻R=10Ω.则如图电路中理想电流表和电压表的读数分别为( )| A. | 2$\sqrt{2}$A,20$\sqrt{2}$V | B. | 2A,20V | C. | 2$\sqrt{2}$A,20V | D. | 2A,20$\sqrt{2}$V |
 长度为L细绳,一端系有一质量为m的小球,小球以O点为圆心在竖直面内做圆周运动,求:
长度为L细绳,一端系有一质量为m的小球,小球以O点为圆心在竖直面内做圆周运动,求: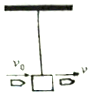 如图所示,用细线挂以质量为M的木块,有一质量为m的子弹自左向右水平射穿此木块,穿透前后子弹的速度分别为vo 和v(设子弹穿过木块的时间和空气阻力不计),求子弹穿出后木块上升的最大高度h.
如图所示,用细线挂以质量为M的木块,有一质量为m的子弹自左向右水平射穿此木块,穿透前后子弹的速度分别为vo 和v(设子弹穿过木块的时间和空气阻力不计),求子弹穿出后木块上升的最大高度h.