题目内容
3. 如图,光滑水平面上有大小相同的小球A和B,A的质量为1kg,B的质量为0.5kg.B用一长为0.4m的细绳悬挂在O点,并与水平面刚好接触,但没有作用力,现给A一定的初速度v,使其向右运动并与B发生弹性碰撞,碰撞B恰好能在竖直平面内完成圆周运动,求:
如图,光滑水平面上有大小相同的小球A和B,A的质量为1kg,B的质量为0.5kg.B用一长为0.4m的细绳悬挂在O点,并与水平面刚好接触,但没有作用力,现给A一定的初速度v,使其向右运动并与B发生弹性碰撞,碰撞B恰好能在竖直平面内完成圆周运动,求:(1)碰撞结束的瞬间B的速度;
(2)碰撞前A的速度;
(3)碰撞结束的瞬间,绳子的拉力.
分析 (1)据题,B恰好能在竖直平面内完成圆周运动,在最高点时,由重力提供向心力,列式求出最高点速度,再由机械能守恒求出碰撞结束的瞬间B的速度.
(2)对于碰撞过程,运用动量守恒和能量守恒求碰撞前A的速度.
(3)碰撞结束的瞬间,根据牛顿第二定律求绳子的拉力.
解答 解:(1)B球在最高点时,有 mBg=mB$\frac{{v}^{2}}{L}$,v=$\sqrt{gL}$=2m/s
碰撞后B球从最低点到最高点的过程,由机械能守恒得 $\frac{1}{2}{m}_{B}{v}_{B}^{2}$=$\frac{1}{2}{m}_{B}{v}^{2}$+2mgL
解得碰撞后B的速度 vB=$\sqrt{5gL}$=$\sqrt{5×10×0.4}$=2$\sqrt{5}$m/s
(2)碰撞过程,取向右为正方向,根据动量守恒得:
mAv=mAvA+mBvB;
由机械能守恒得
$\frac{1}{2}{m}_{A}{v}_{A}^{2}$=$\frac{1}{2}{m}_{A}{v}_{A}^{2}$+$\frac{1}{2}{m}_{B}{v}_{B}^{2}$
联立解得 v=$\frac{({m}_{A}+{m}_{B}){v}_{B}}{2{m}_{A}}$=$\frac{(1+0.5)×2\sqrt{5}}{2×1}$=$\frac{3\sqrt{5}}{2}$m/s
(3)碰撞结束的瞬间,对B球,由牛顿第二定律得 T-mBg=mB$\frac{{v}_{B}^{2}}{L}$
解得绳子的拉力 T=6mBg=6×0.5×10N=30N
答:
(1)碰撞结束的瞬间B的速度是2$\sqrt{5}$m/s;
(2)碰撞前A的速度是$\frac{3\sqrt{5}}{2}$m/s;
(3)碰撞结束的瞬间,绳子的拉力是30N.
点评 本题主要考查了机械能守恒定律、动量守恒定律及向心力公式的直接应用,要求同学们能在最高点对摆球进行正确的受力分析,掌握临界条件,知道弹性碰撞遵守两大守恒:动量守恒和机械能守恒.

 如图所示,左侧的圆形导电环半径为r=2.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容为C=100μF的电容器相接,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁场磁感应强度B的变化率$\frac{△B}{△t}$=100$\sqrt{2}$πsinωt,若电容器C所带电荷量的最大值为1.41×10-9C,则所用理想变压器的原副线圈的匝数之比是(取π2=10)( )
如图所示,左侧的圆形导电环半径为r=2.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容为C=100μF的电容器相接,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁场磁感应强度B的变化率$\frac{△B}{△t}$=100$\sqrt{2}$πsinωt,若电容器C所带电荷量的最大值为1.41×10-9C,则所用理想变压器的原副线圈的匝数之比是(取π2=10)( )| A. | 25:1 | B. | 1:25 | C. | 141:4 | D. | 4:141 |
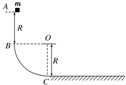 如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )
如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )| A. | 0.1m | B. | 0.2m | C. | 0.6m | D. | 0.8m |
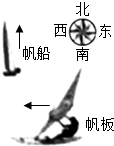
| A. | 帆船朝正东方向航行,速度大小为v | |
| B. | 帆船朝正西方向航行,速度大小为v | |
| C. | 帆船朝南偏东45°方向航行,速度大小为$\sqrt{2}$v | |
| D. | 帆船朝北偏东45°方向航行,速度大小为$\sqrt{2}$v |

 氦原子被电离出一个核外电子,形成类氢结构的氦离子,已知基态的一价氦离子能量为E1=-54.4eV,能级图如图所示,则一价氦离子第α能级En=$\frac{-54.4}{{n}^{2}}$eV;一个静止的处于基态的一价氦离子被运动的电子碰撞后又失去了一个电子,则运动电子的动能一定大于54.4eV.
氦原子被电离出一个核外电子,形成类氢结构的氦离子,已知基态的一价氦离子能量为E1=-54.4eV,能级图如图所示,则一价氦离子第α能级En=$\frac{-54.4}{{n}^{2}}$eV;一个静止的处于基态的一价氦离子被运动的电子碰撞后又失去了一个电子,则运动电子的动能一定大于54.4eV. 如图所示,水平地面上固定一木板,小滑块A质量为m,带电量为+q,与木板之间没有摩擦力;小滑块B质量为3m,不带电,与木板之间的摩擦因数μ=0.5;木板左边界MN和PQ之间的距离为l,其间存在匀强电场,电场强度E满足qE=mg.B静止在边界PQ处,将A从木板左端静止释放,此后A、B会发生碰撞,每次碰撞均为弹性碰撞,且碰撞前后A、B的电量保持不变,A、B均可视为质点,重力加速度为g.
如图所示,水平地面上固定一木板,小滑块A质量为m,带电量为+q,与木板之间没有摩擦力;小滑块B质量为3m,不带电,与木板之间的摩擦因数μ=0.5;木板左边界MN和PQ之间的距离为l,其间存在匀强电场,电场强度E满足qE=mg.B静止在边界PQ处,将A从木板左端静止释放,此后A、B会发生碰撞,每次碰撞均为弹性碰撞,且碰撞前后A、B的电量保持不变,A、B均可视为质点,重力加速度为g.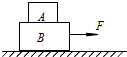 如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右匀速运动,设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.若水平外力F突然增大,但A、B仍保持相对静止,设此时A、B之间的摩擦力为f3,B与水平桌面间的摩擦力为f4,则( )
如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右匀速运动,设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.若水平外力F突然增大,但A、B仍保持相对静止,设此时A、B之间的摩擦力为f3,B与水平桌面间的摩擦力为f4,则( ) 图为某种离子加速器的设计方案.两个半圆形金属盒内存在相同的垂直于纸面向外的匀强磁场.其中MN和M′N′是间距为h的两平行极板,其上分别有正对的两个小孔O和O′,O′N′=ON=d,P为靶点,O′P=kd(k为大于1的整数).极板间存在方向向上的匀强电场,两极板间电压为U.质量为m、带电量为q的正离子从O点由静止开始加速,经O′进入磁场区域.当离子打到极板上O′N′区域(含N′点)或外壳上时将会被吸收.两虚线之间的区域无电场和磁场存在,离子可匀速穿过.忽略相对论效应和离子所受的重力.求:
图为某种离子加速器的设计方案.两个半圆形金属盒内存在相同的垂直于纸面向外的匀强磁场.其中MN和M′N′是间距为h的两平行极板,其上分别有正对的两个小孔O和O′,O′N′=ON=d,P为靶点,O′P=kd(k为大于1的整数).极板间存在方向向上的匀强电场,两极板间电压为U.质量为m、带电量为q的正离子从O点由静止开始加速,经O′进入磁场区域.当离子打到极板上O′N′区域(含N′点)或外壳上时将会被吸收.两虚线之间的区域无电场和磁场存在,离子可匀速穿过.忽略相对论效应和离子所受的重力.求: