题目内容
18．
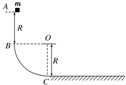如图所示，BC是竖直面内的四分之一圆弧形光滑轨道，下端C与水平直轨道相切．一个小物块从B点正上方R处的A点处由静止释放，从B点刚好进入圆弧形光滑轨道下滑，已知圆弧形轨道半径为R=0.2m，小物块的质量为m=0.1kg，小物块与水平面间的动摩擦因数μ=0.5，取g=10m/s2．小物块在水平面上滑动的最大距离是（ ）| A． | 0.1m | B． | 0.2m | C． | 0.6m | D． | 0.8m |
分析 从小物块从A点开始运动到停止全过程运用动能定理，在此过程中有重力做功，摩擦力做功，动能的变化为0，根据动能定理求出滑动的最大距离
解答 解：设在水平面上滑动的最大距离为s，由动能定理得：
mg•2R-μmgs=0
解得：s=$\frac{2R}{μ}$=$\frac{2×0.2}{0.5}$=0.8m 则D正确
故选：D
点评 解决本题的关键明确由重力与摩擦力做功，用动能定理进行解题．
练习册系列答案
相关题目
8．电磁灶是利用电磁感应原理加热的一种新型灶具，下列对电磁灶的相关说法中正确的是（ ）
| A． | 加热用锅体其材料可采用陶瓷 | |
| B． | 锅体中的涡流是由恒定的磁场产生的 | |
| C． | 锅体中的涡流是由变化的磁场产生的 | |
| D． | 提高磁场变化的频率，可提高电磁灶的加热效果 |
9．在用“油膜法测量油酸分子大小”的实验中，下列说法中正确的是（ ）
| A． | 用油膜法可以精确测量分子的大小 | |
| B． | 油酸分子直径等于纯油酸体积除以相应油膜面积 | |
| C． | 计算油膜面积时，应舍去所有不足一格的方格 | |
| D． | 实验时应先将一滴油酸酒精溶液滴入水面，再把痱子粉洒在水面上 |
13．建立物理模型是物理研究的常用方法，下列属于理想化“物理模型”的是（ ）
| A． | 重力 | B． | 向心力 | C． | 元电荷 | D． | 点电荷 |
如图，光滑水平面上有大小相同的小球A和B，A的质量为1kg，B的质量为0.5kg．B用一长为0.4m的细绳悬挂在O点，并与水平面刚好接触，但没有作用力，现给A一定的初速度v，使其向右运动并与B发生弹性碰撞，碰撞B恰好能在竖直平面内完成圆周运动，求：
10．
如图所示电路中，电源电动势为E内阻为r，当滑动变阻器R2滑动端向右滑动后，理想电流表A1、A2的示数变化量的绝对值分别为△I1、△I2，理想电压表示数变化量的绝对值为△U．下列说法中正确的是（ ）
如图所示电路中，电源电动势为E内阻为r，当滑动变阻器R2滑动端向右滑动后，理想电流表A1、A2的示数变化量的绝对值分别为△I1、△I2，理想电压表示数变化量的绝对值为△U．下列说法中正确的是（ ）| A． | 电压表V的示数减小 | B． | 电流表A2的示数变小 | ||
| C． | △U与△I1比值一定小于电源内阻r | D． | △U与△I2比值一定小于电源内阻r |
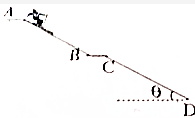如图所示为一滑雪跳台，滑雪运动员从A点由静止开始下滑至C点飞出，设从A至C运动员只滑行，BC段水平，CD段与水平面成θ角，tanθ=$\frac{3}{4}$，A、B的竖直高度差是40m，雪面和空气阻力忽略不计，求滑雪运动员落在CD段上的位置．
如图所示，让质量为m=0.2kg图中的位置A由静止开始下摆，正好摆到最低点B时摆线被拉断．设摆线长l=1.5m，悬点到地面的高度为h=6.5m，不计空气阻力．（g=10m/s2）