题目内容
9. 如图所示,质量为m的木块在与水平方向成α角斜向上的拉力F作用下从静止 开始沿水平地面滑动.若木块与地面间的动摩擦因数为μ.求:
如图所示,质量为m的木块在与水平方向成α角斜向上的拉力F作用下从静止 开始沿水平地面滑动.若木块与地面间的动摩擦因数为μ.求:(1)木块的加速度;
(2)经过时间t,木块滑动的距离.
分析 对物体受力分析,抓住竖直方向上的合力为零,根据牛顿第二定律求出物体的加速度.由位移公式可求得位移.
解答 解: 对物体受力分析可知,物体受到重力、支持力、拉力和摩擦力的作用,
对物体受力分析可知,物体受到重力、支持力、拉力和摩擦力的作用,
在水平方向有:Fcosα-f=Ma,
竖直方向有:Mg=FN+Fsinα,
滑动摩擦力:f=μFN,
得滑动摩擦力大小:Ff=μ(mg-Fsinα)
加速度大小a=$\frac{Fcosα-μ(mg-Fsinα)}{m}$
(2)经过时间t的位移x=$\frac{1}{2}a{t}^{2}$=$\frac{1}{2}×$$\frac{Fcosα-μ(mg-Fsinα)}{m}$t2=$\frac{[Fcosα-μ(mg-Fsinα)]{t}^{2}}{2m}$
答:(1)加速度大小为$\frac{Fcosα-μ(mg-Fsinα)}{m}$.
(2)经过t的位移为$\frac{[Fcosα-μ(mg-Fsinα)]{t}^{2}}{2m}$
点评 本题就是考查学生对牛顿第二定律的基本的应用,通过受力分析列式即可求得.注意压力为重力与拉力向上的分力的合力.

练习册系列答案
相关题目
19.下列关于静电的叙述,正确的是( )
| A. | 感应起电说明物体创造了电荷 | |
| B. | 点电荷是一种理想模型 | |
| C. | 验电器是利用异种电荷相互排斥原理制成的 | |
| D. | 库仑测定了元电荷的电荷量 |
5.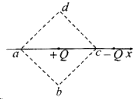 如图所示,在x轴上固定两个等量异种点电荷+Q、-Q,两点电荷之间距离L,虚线是以+Q所在点为中心,边长为L的正方形,a、b、c、d为正方形的四个顶点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
如图所示,在x轴上固定两个等量异种点电荷+Q、-Q,两点电荷之间距离L,虚线是以+Q所在点为中心,边长为L的正方形,a、b、c、d为正方形的四个顶点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
 如图所示,在x轴上固定两个等量异种点电荷+Q、-Q,两点电荷之间距离L,虚线是以+Q所在点为中心,边长为L的正方形,a、b、c、d为正方形的四个顶点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
如图所示,在x轴上固定两个等量异种点电荷+Q、-Q,两点电荷之间距离L,虚线是以+Q所在点为中心,边长为L的正方形,a、b、c、d为正方形的四个顶点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )| A. | 四点中c点处的电势最低 | |
| B. | a,b两点的电势差Uab大于a,d两点的电势差Uad | |
| C. | 将一正试探电荷沿a→b→c从a移至c点,电势能先增大后减小 | |
| D. | a点电场强度的大小Ea大于c点的电场强度的大小Ec |
2.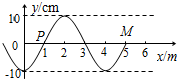 如图所示,一列简谐横波沿x轴正方向传播,从波传到x=5m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4s,下面说法中正确的是( )
如图所示,一列简谐横波沿x轴正方向传播,从波传到x=5m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4s,下面说法中正确的是( )
 如图所示,一列简谐横波沿x轴正方向传播,从波传到x=5m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4s,下面说法中正确的是( )
如图所示,一列简谐横波沿x轴正方向传播,从波传到x=5m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4s,下面说法中正确的是( )| A. | 质点Q(x=9m,图中未画出)经过0.5s第一次到达波谷 | |
| B. | 质点P在0.1s内沿波传播方向的位移为1m | |
| C. | 若在Q处放一接收器,接到的波的频率小于2.5Hz | |
| D. | 若该波传播中遇到宽约3m的障碍物能发生明显的衍射现象 |
3.下列有关力的说法中正确的是( )
| A. | 静止在水平面上的物体对水平面的压力就是物体的重力 | |
| B. | 两个力的合力可能小于其中的任一个分力 | |
| C. | 静止在水平面上的物体所受的支持力和它对水平面的压力相互平衡 | |
| D. | 在斜面上匀速下滑的物体受到重力、支持力、摩擦力和下滑力的作用 |
 如图所示,物体的质量m=4kg,与水平面的摩擦因数为μ=0.4,在倾角为37°大小为100N的恒力F的作用下由静止开始加速运动(已知sin37°=0.6,cos37°=0.8,g=10m/s2)试求:
如图所示,物体的质量m=4kg,与水平面的摩擦因数为μ=0.4,在倾角为37°大小为100N的恒力F的作用下由静止开始加速运动(已知sin37°=0.6,cos37°=0.8,g=10m/s2)试求: 如图所示,一质量m=2kg的物体静止在水平地面上,它与地面间的动摩擦因数μ=0.2,现用一水平向右的恒力F推物体,使其做匀加速运动,经时间t=4s撤去推力F时物体的速度V=12m/s.物体又向前滑行了一段距离后停止运动,取g=10m/s2,试求:
如图所示,一质量m=2kg的物体静止在水平地面上,它与地面间的动摩擦因数μ=0.2,现用一水平向右的恒力F推物体,使其做匀加速运动,经时间t=4s撤去推力F时物体的速度V=12m/s.物体又向前滑行了一段距离后停止运动,取g=10m/s2,试求: 如图所示,质量为m=10kg的物块,在F=30N的水平拉力作用下,从静止开始沿水平面运动t1=4s后撤去拉力,已知物块与水平面间的动摩擦因数为μ=0.2,g取10m/s2.求:
如图所示,质量为m=10kg的物块,在F=30N的水平拉力作用下,从静止开始沿水平面运动t1=4s后撤去拉力,已知物块与水平面间的动摩擦因数为μ=0.2,g取10m/s2.求: