题目内容
11. 如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )
如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )| A. | 导体棒MN经过区域I时,导体棒中的电流由M流向N | |
| B. | 导体棒MN经过区域II时,导体棒MN受到的安培力方向向右 | |
| C. | 导体棒MN经过区域II时,R两端的电压是3V | |
| D. | 通过R的电流是交变电流,有效值为$\frac{{\sqrt{10}}}{2}A$ |
分析 根据右手定则判断电流方向,根据左手定则判断导体棒MN受到的安培力方向;根据E=BLv计算导体棒MN产生的感应电动势,根据闭合电路的欧姆定律计算R两端的电压;根据有效值的概念计算电动势有效值,再计算电流强度有效值.
解答 解:A、根据右手定则可知,导体棒MN经过区域I时,导体棒中的电流由N流向M,A错误;
B、导体棒MN经过区域II时,根据右手定则可知电流方向由M到N,根据左手定则可知导体棒MN受到的安培力方向向左,B错误;
C、导体棒MN经过区域II时,产生的感应电动势E2=B2Lv=1×4×1V=4V,R两端的电压是U=$\frac{{E}_{2}}{R+r}•R=\frac{4}{1.5+0.5}×1.5V=3V$,C正确;
D、通过区域I时感应电动势E1=$\frac{1}{2}{E}_{2}=2V$,设电压有效值为E,则$\frac{{E}^{2}}{{R}_{总}}T$=$\frac{{{E}_{1}}^{2}}{{R}_{总}}•\frac{T}{2}$+$\frac{{{E}_{2}}^{2}}{{R}_{总}}•\frac{T}{2}$,解得:E=$\sqrt{10}V$,则电流强度的有效值为:I=$\frac{E}{R+r}=\frac{\sqrt{10}}{2}A$,D正确.
故选:CD.
点评 对于导体切割磁感应线产生的感应电动势情况有两种:一是导体平动切割产生的感应电动势,可以根据E=BLv来计算;二是导体棒转动切割磁感应线产生的感应电动势,可以根据$\frac{1}{2}B{L}^{2}ω$来计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.某质点的v-t图象如图所示,则( )


| A. | 前2s质点做匀加速直线运动 | B. | 4~6 s内质点匀速直线运动 | ||
| C. | 3 s末质点速度是5 m/s | D. | 8 s末质点回到原出发点 |
11.下列说法正确的是( )
| A. | 给电风扇供电时,电能全部转化为机械能 | |
| B. | 给电风扇供电时,电能主要转化为内能 | |
| C. | 给电热器供电时,电能几乎全部转化为内能 | |
| D. | 给电热器供电时,只有很少一部分电能转化为内能 |
6.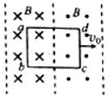 如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )
如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )
 如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )
如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )| A. | 穿过回路磁通量的变化率为零 | |
| B. | 回路中感应电动势大小为Blv0 | |
| C. | 回路中感应电流的方向为a→b→c→d方向 | |
| D. | 回路中ab边与cd边所受安培力方向相同 |
16. 如图所示,一导线弯成半径为a的半圆形闭合回路,虚线MN右侧有磁感应强度为B的匀强磁场.方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成半径为a的半圆形闭合回路,虚线MN右侧有磁感应强度为B的匀强磁场.方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )
 如图所示,一导线弯成半径为a的半圆形闭合回路,虚线MN右侧有磁感应强度为B的匀强磁场.方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成半径为a的半圆形闭合回路,虚线MN右侧有磁感应强度为B的匀强磁场.方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )| A. | 感应电流方向不变 | B. | CD段直线始终不受安培力 | ||
| C. | 感应电动势最大值Em=Bav | D. | 感应电动势平均值$\overline{E}$=$\frac{1}{4}$Bav |
3.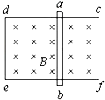 如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
 如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )| A. | 金属棒中的感应电流的方向为b→a | |
| B. | 金属棒中的感应电流的大小为$\frac{{k{l^{\;}}}}{r}$ | |
| C. | 金属棒消耗的电功率为$\frac{{k}^{2}{l}^{4}}{r}$ | |
| D. | 若t=t1时金属棒仍然静止,金属棒受到的最大静摩擦力不能小于(B0+kt1)$\frac{{k{l^3}}}{r}$ |
20.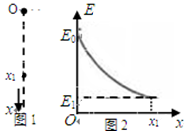 某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
 某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )| A. | 从O到x1的过程中,小球的速率越来越大,加速度越来越大 | |
| B. | 电场强度大小恒定,方向沿x轴负方向 | |
| C. | 从O到x1的过程中,相等的位移内,小球克服电场力做的功相等 | |
| D. | 到达x1位置时,小球速度的大小为$\sqrt{\frac{2({E}_{1}-{E}_{0}+mg{x}_{1})}{m}}$ |
1.在如图所示的电路中,当滑动变阻器R3的滑动触头P向下滑动时( )


| A. | 电压表示数变小 | B. | 电压表示数变大 | C. | 电流表示数变小 | D. | 电流表示数变大 |
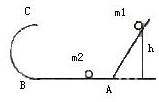 如图所示半圆轨道直径BC=0.8m,水平轨道上AB=1.6m.m1,m2均为0.1kg的弹性球.若m1由高h处开始下滑与静止在A处的球m2发生正碰,碰后m2运动经C点抛出后又与m1相碰,求:
如图所示半圆轨道直径BC=0.8m,水平轨道上AB=1.6m.m1,m2均为0.1kg的弹性球.若m1由高h处开始下滑与静止在A处的球m2发生正碰,碰后m2运动经C点抛出后又与m1相碰,求: