题目内容
6.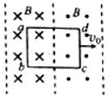 如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )
如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )| A. | 穿过回路磁通量的变化率为零 | |
| B. | 回路中感应电动势大小为Blv0 | |
| C. | 回路中感应电流的方向为a→b→c→d方向 | |
| D. | 回路中ab边与cd边所受安培力方向相同 |
分析 分析清楚图示情景判断磁通量与变化率大小,应用E=BLv求出感应电动势,应用右手定则判断出感应电流方向,应用左手定则判断出安培力方向.
解答 解:A、在图示位置,穿过回路的磁通量为零但磁通量的变化率不为零,故A错误;
B、ab与cd两边都切割磁感线,回路感应电动势大小为:E=2Blv0,故B错误;
C、由右手定则或楞次定律可知,感应电流方向为:a→d→c→b→a,故C错误;
D、由左手定则可知,ab与cd边受到的安培力方向都水平向左,两边所受安培力方向相同,故D正确;
故选:D.
点评 本题考查了判断磁通量变化率、求感应电动势、判断感应电流方向、判断安培力方向问题,涉及的知识点较多但难度不大,掌握基础知识即可解题,平时要注意基础知识的学习与掌握.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
6.关于电场线的说法正确的是( )
| A. | 电场线是为了形象的描述电场而假设的线 | |
| B. | 电场线就是电荷在电场中的运动轨迹 | |
| C. | 电场线是闭合的曲线 | |
| D. | 两条电场线在电场中可以相交 |
3.长为5m的竖直杆下端距离一竖直隧道口为15m,让这根杆自由下落,它全部通过隧道口的时间为(g取10m/s2)( )
| A. | 2s | B. | $\sqrt{3}$s | C. | (2-$\sqrt{3}$)s | D. | ($\sqrt{3}$+1)s |
11. 如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )
如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )
 如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )
如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )| A. | 导体棒MN经过区域I时,导体棒中的电流由M流向N | |
| B. | 导体棒MN经过区域II时,导体棒MN受到的安培力方向向右 | |
| C. | 导体棒MN经过区域II时,R两端的电压是3V | |
| D. | 通过R的电流是交变电流,有效值为$\frac{{\sqrt{10}}}{2}A$ |
15. 平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )
平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )
 平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )
平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )| A. | 微粒带负电 | B. | 动能逐渐增加 | ||
| C. | 电势能逐渐增加 | D. | 重力势能逐渐增加 |
16.对于闭合电路欧姆定律的理解,下列说法一定正确的是( )
| A. | 在电源电动势不变时,外电路的电阻越大,路端电压越大 | |
| B. | 在电源电动势不变时,外电路的电阻越大,电源内电压越大 | |
| C. | 当外电路断开时,路端电压的大小等于电源电动势 | |
| D. | 当外电路短路时,电源电动势为零 |
 如图甲所示,两根足够长的平行导轨处在与水平方向成θ=37°角的斜面上,两导轨间距L=0.3m.导轨两端各接一个阻值R0=2Ω的电阻;在斜面上加有磁感应强度B=1T、方向垂直于导轨平面的匀强磁场.一质量m=1kg、电阻r=2Ω的金属棒横跨在平行导轨间,棒与导轨间的动摩擦因数μ=0.5,金属棒以v0=10m/s的初速度上滑,直至上升到最高点的过程中,通过上端电阻的电荷量q=0.1C,已知g取10m/s2,sin37°=0.6,cos37°=0.8,其余电阻不计.求:
如图甲所示,两根足够长的平行导轨处在与水平方向成θ=37°角的斜面上,两导轨间距L=0.3m.导轨两端各接一个阻值R0=2Ω的电阻;在斜面上加有磁感应强度B=1T、方向垂直于导轨平面的匀强磁场.一质量m=1kg、电阻r=2Ω的金属棒横跨在平行导轨间,棒与导轨间的动摩擦因数μ=0.5,金属棒以v0=10m/s的初速度上滑,直至上升到最高点的过程中,通过上端电阻的电荷量q=0.1C,已知g取10m/s2,sin37°=0.6,cos37°=0.8,其余电阻不计.求: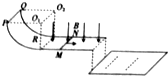 如图所示,电阻不计的两光滑金属导轨相距L固定在水平绝缘桌面上,其中半径为R的$\frac{1}{4}$圆弧部分处在竖直平面内,水平直导轨部分处在磁感应强度为B、方向竖直向下的匀强磁场中,末端平齐.在与圆心等高的位置处有两金属棒MN、PQ垂直两导轨且与导轨接触良好.已知MN棒的质量为2m,电阻为r;PQ棒的质量为m,电阻也为r.开始时,保持PQ棒不动,将MN棒从圆弧导轨顶端无初速度释放,当MN棒脱离导轨后,再次由静止释放PQ棒,最后两棒都离开导轨落到地面上.MN、PQ两棒落地点到导轨边缘的水平距离之比为1:3.
如图所示,电阻不计的两光滑金属导轨相距L固定在水平绝缘桌面上,其中半径为R的$\frac{1}{4}$圆弧部分处在竖直平面内,水平直导轨部分处在磁感应强度为B、方向竖直向下的匀强磁场中,末端平齐.在与圆心等高的位置处有两金属棒MN、PQ垂直两导轨且与导轨接触良好.已知MN棒的质量为2m,电阻为r;PQ棒的质量为m,电阻也为r.开始时,保持PQ棒不动,将MN棒从圆弧导轨顶端无初速度释放,当MN棒脱离导轨后,再次由静止释放PQ棒,最后两棒都离开导轨落到地面上.MN、PQ两棒落地点到导轨边缘的水平距离之比为1:3.