题目内容
16. 如图所示,一导线弯成半径为a的半圆形闭合回路,虚线MN右侧有磁感应强度为B的匀强磁场.方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成半径为a的半圆形闭合回路,虚线MN右侧有磁感应强度为B的匀强磁场.方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )| A. | 感应电流方向不变 | B. | CD段直线始终不受安培力 | ||
| C. | 感应电动势最大值Em=Bav | D. | 感应电动势平均值$\overline{E}$=$\frac{1}{4}$Bav |
分析 由楞次定律可判断电流方向,根据导线与磁场方向关系分CD段是否受安培力;由E=BLv,分析过程中最长的有效切割长度,即可求得感应电动势最大值;由法拉第电磁感应定律可得出感应电动势的平均值.
解答 解:A、在闭合电路进入磁场的过程中,穿过闭合电路的磁通量逐渐增大,根据楞次定律可知,感应电流的方向为逆时针方向不变,故A正确.
B、线框进入磁场的过程中产生感应电流,由于CD段与磁场垂直,所以CD段直线始终受到安培力,故B错误.
C、当闭合回路进入磁场一半时,这时有效的切割长度最大,为a,所以感应电动势最大 Em=Bav,故C正确.
D、由法拉第电磁感应定律可得,感应电动势平均值 $\overline{E}$=$\frac{△Φ}{△t}$=$\frac{B•\frac{1}{2}π{a}^{2}}{\frac{2a}{v}}$=$\frac{1}{4}$πBav,故D错误.
故选:AC
点评 本题注意以下几点:(1)感应电动势公式E=$\frac{△Φ}{△t}$一般用来计算感应电动势的平均值;(2)利用感应电动势公式E=Blv计算时,l应是有效的切割长度,即垂直切割磁感线的长度.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
15.为了研究超重与失重现象,某同学把一体重秤放在电梯的地板上,他站在体重秤上随电梯运动并观察体重秤示数的变化情况.下表记录了几个特定时刻体重秤的示数.若已知t0时刻电梯静止,则( )
| 时间 | t0 | t1 | t2 | t3 |
| 体重秤示数(kg) | 45.0 | 50.0 | 40.0 | 45.0 |
| A. | t1和t2时刻该同学的质量并没有变化,所受重力不发生变化 | |
| B. | t1和t2时刻电梯的加速度方向一定相反 | |
| C. | t1和t2时刻电梯运动方向一定相反 | |
| D. | t2时刻电梯的加速度一定为零 |
4. 一边长为L、电阻为R的正方形单匝线框沿光滑水平面运动,以速度v1开始进入一磁感应强度为B的有界匀强磁场区域,最终以速度v2滑出磁场.设线框在运动过程中速度方向始终与磁场边界垂直,磁场的宽度大于L(如图所示).刚进入磁场瞬时,线框中的感应电流为I1.下列说法正确的是( )
一边长为L、电阻为R的正方形单匝线框沿光滑水平面运动,以速度v1开始进入一磁感应强度为B的有界匀强磁场区域,最终以速度v2滑出磁场.设线框在运动过程中速度方向始终与磁场边界垂直,磁场的宽度大于L(如图所示).刚进入磁场瞬时,线框中的感应电流为I1.下列说法正确的是( )
 一边长为L、电阻为R的正方形单匝线框沿光滑水平面运动,以速度v1开始进入一磁感应强度为B的有界匀强磁场区域,最终以速度v2滑出磁场.设线框在运动过程中速度方向始终与磁场边界垂直,磁场的宽度大于L(如图所示).刚进入磁场瞬时,线框中的感应电流为I1.下列说法正确的是( )
一边长为L、电阻为R的正方形单匝线框沿光滑水平面运动,以速度v1开始进入一磁感应强度为B的有界匀强磁场区域,最终以速度v2滑出磁场.设线框在运动过程中速度方向始终与磁场边界垂直,磁场的宽度大于L(如图所示).刚进入磁场瞬时,线框中的感应电流为I1.下列说法正确的是( )| A. | 线框完全在磁场中时的运动速度v=$\frac{{{v_1}-{v_2}}}{2}$ | |
| B. | 线框滑出磁场时的电流I2=$\frac{{{v_1}{I_1}}}{v_2}$ | |
| C. | 进入磁场的过程中,通过线框的电量q=$\frac{{L{I_1}}}{v_1}$ | |
| D. | 整个穿越磁场的过程中通过线框的总电量Q=$\frac{{B{L^2}}}{R}$ |
11. 如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )
如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )
 如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )
如图所示,足够长金属导轨水平放置,做短连接定值电阻R=1.5Ω.导轨间距为L=4m,其间有足够多等间距反向分布的磁场区域I和II,磁感应强度大小分别为B1=0.5T和B2=1T.方向都垂直于导轨所在平面.长度也为L的导体棒MN也沿导轨以速度v=1m/s匀速向右滑动,始终与导轨垂直且接触良好,导体棒电阻r=0.5Ω.不计导轨的电阻.下列说法正确的是( )| A. | 导体棒MN经过区域I时,导体棒中的电流由M流向N | |
| B. | 导体棒MN经过区域II时,导体棒MN受到的安培力方向向右 | |
| C. | 导体棒MN经过区域II时,R两端的电压是3V | |
| D. | 通过R的电流是交变电流,有效值为$\frac{{\sqrt{10}}}{2}A$ |
5. 如图所示的直角坐标系中,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方,取无穷远处的电势为零.下列说法正确的是( )
如图所示的直角坐标系中,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方,取无穷远处的电势为零.下列说法正确的是( )
 如图所示的直角坐标系中,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方,取无穷远处的电势为零.下列说法正确的是( )
如图所示的直角坐标系中,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方,取无穷远处的电势为零.下列说法正确的是( )| A. | b点的电势为零,电场强度也为零 | |
| B. | 正的试探电荷在a点的电势能大于零,所受电场力方向向右 | |
| C. | 将正的试探电荷从O点移到a点,电势能减少 | |
| D. | 将同一正的试探电荷先后分别从O、b点移到a点,第二次电势能的变化较大 |
 如图甲所示,两根足够长的光滑平行金属导轨相距l=0.4 m,导轨平面与水平面成θ=30°角,下端通过导线连接阻值R=0.5Ω的电阻.金属棒ab阻值r=0.3Ω,质量m=0.2kg,放在两导轨上,与导轨垂直并保持良好接触.其余部分电阻不计,整个装置处于垂直导轨平面向上的匀强磁场中.取g=10 m/s2.
如图甲所示,两根足够长的光滑平行金属导轨相距l=0.4 m,导轨平面与水平面成θ=30°角,下端通过导线连接阻值R=0.5Ω的电阻.金属棒ab阻值r=0.3Ω,质量m=0.2kg,放在两导轨上,与导轨垂直并保持良好接触.其余部分电阻不计,整个装置处于垂直导轨平面向上的匀强磁场中.取g=10 m/s2.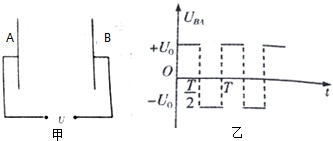
 如图所示,一个质量为10kg的物体挂在弹簧上,弹簧伸长了0.2m,再将弹簧拉长0.1m,然后放开,求弹簧的运动规律(设阻尼系数为0).
如图所示,一个质量为10kg的物体挂在弹簧上,弹簧伸长了0.2m,再将弹簧拉长0.1m,然后放开,求弹簧的运动规律(设阻尼系数为0).