题目内容
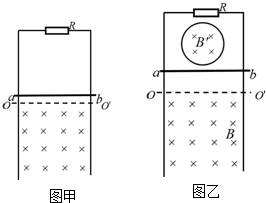
6. 如图,一对表面粗糙的平行金属轨道竖直固定在水平地面上,轨道与地面绝缘,轨道顶端连接有一定值电阻R,在A1A2、A3A4区域内有垂直于轨道平面向里的匀强磁场,一水平金属杆CD通过两金属环套在轨道上,现使金属杆CD以某一初速度竖直向上运动,穿过磁场区域后继续上升到最高位置A5A6,然后落回到地面,此后不再运动,已知金属杆CD与轨道间的摩擦力大小恒为其重力的$\frac{1}{3}$倍,金属杆C向上运动经过A1A2和A3A4位置时,速度之比为2:1,A3A4与A5A6间的距离是A1A2与A3A4间的距离的n倍,金属杆CD向下运动刚进入磁场区域就做匀速运动,重力加速度为g,金属轨道与金属杆CD的电阻都忽略不计.求:
如图,一对表面粗糙的平行金属轨道竖直固定在水平地面上,轨道与地面绝缘,轨道顶端连接有一定值电阻R,在A1A2、A3A4区域内有垂直于轨道平面向里的匀强磁场,一水平金属杆CD通过两金属环套在轨道上,现使金属杆CD以某一初速度竖直向上运动,穿过磁场区域后继续上升到最高位置A5A6,然后落回到地面,此后不再运动,已知金属杆CD与轨道间的摩擦力大小恒为其重力的$\frac{1}{3}$倍,金属杆C向上运动经过A1A2和A3A4位置时,速度之比为2:1,A3A4与A5A6间的距离是A1A2与A3A4间的距离的n倍,金属杆CD向下运动刚进入磁场区域就做匀速运动,重力加速度为g,金属轨道与金属杆CD的电阻都忽略不计.求:(1)金属杆CD向上,向下两次经过A3A4位置时的速度之比;
(2)金属杆CD向上运动经过A1A2刚进入磁场时的加速度大小;
(3)金属杆CD向上、向下两次经过磁场区域的过程中定值电阻R上产生的焦耳热之比.
分析 (1)根据牛顿第二定律求出经过${A}_{3}^{\;}{A}_{4}^{\;}$向上的加速度,和下降时的加速度,由运动学公式求出金属杆CD向上,向下两次经过A3A4位置时的速度之比
(2)杆向上经过${A}_{1}^{\;}{A}_{2}^{\;}$时切割磁感线产生感应电动势,受到向下的安培力,根据牛顿第二定律列式,向下进入磁场做匀速运动受力平衡,结合(1),即可求出金属杆CD向上运动经过A1A2刚进入磁场时的加速度大小
(3)根据动能定理求出CD向上经过磁场区域过程中克服安培力做的功,下降过程匀速通过磁场,根据功的公式求出克服安培力做的功,两种情况下克服安培力做功之比即为定值电阻R上产生的焦耳热之比
解答 解:(1)设杆的质量为m,${A}_{3}^{\;}{A}_{4}^{\;}$与${A}_{5}^{\;}{A}_{6}^{\;}$间的距离为h,上升过程中的加速度大小为:
${a}_{1}^{\;}=\frac{mg+\frac{1}{3}mg}{m}=\frac{4}{3}g$
又$0-{v}_{1}^{2}=-2{a}_{1}^{\;}h$
则${v}_{1}^{\;}=\sqrt{\frac{8}{3}gh}$
下降过程中的加速度大小为${a}_{2}^{\;}=\frac{mg-\frac{1}{3}mg}{m}=\frac{2}{3}g$
又${v}_{2}^{2}-0=2{a}_{2}^{\;}h$
则${v}_{2}^{\;}=\sqrt{\frac{4}{3}gh}$
则:${v}_{1}^{\;}:{v}_{2}^{\;}=\sqrt{2}:1$
(2)设杆的长度为l,杆向上运动经过${A}_{1}^{\;}{A}_{2}^{\;}$时的速度为${v}_{0}^{\;}$,切割产生的电动势
${E}_{1}^{\;}=Bl{v}_{0}^{\;}$
回路中的电流${I}_{1}^{\;}=\frac{{E}_{1}^{\;}}{R}=\frac{Bl{v}_{0}^{\;}}{R}$
杆受到的安培力大小为${F}_{1}^{\;}=B{I}_{1}^{\;}l=\frac{{B}_{\;}^{2}{l}_{\;}^{2}{v}_{0}^{\;}}{R}$,方向竖直向下
杆向上运动经过${A}_{1}^{\;}{A}_{2}^{\;}$刚进入磁场时,由牛顿第二定律:$mg+\frac{1}{3}mg+{F}_{1}^{\;}=ma$
得$a=\frac{4}{3}g+\frac{{F}_{1}^{\;}}{m}$
由题意,杆下落进入磁场做匀速运动的速度为${v}_{2}^{\;}$,
切割产生的电动势${E}_{2}^{\;}=Bl{v}_{2}^{\;}$
此时回路中的电流${I}_{2}^{\;}=\frac{{E}_{2}^{\;}}{R}=\frac{Bl{v}_{2}^{\;}}{R}$
杆受到的安培力大小为${F}_{2}^{\;}=B{I}_{2}^{\;}l=\frac{{B}_{\;}^{2}{l}_{\;}^{2}{v}_{2}^{\;}}{R}$
这一过程中杆受力平衡,即${F}_{2}^{\;}+\frac{1}{3}mg=mg$
可得${F}_{2}^{\;}=\frac{{B}_{\;}^{2}{l}_{\;}^{2}{v}_{2}^{\;}}{R}=\frac{2}{3}mg$
由(1)问${v}_{1}^{\;}:{v}_{2}^{\;}=\sqrt{2}:1$,又${v}_{0}^{\;}=2{v}_{1}^{\;}$,可得${v}_{0}^{\;}=2\sqrt{2}{v}_{2}^{\;}$
代入可得$a=\frac{4+4\sqrt{2}}{3}g$
(3)设${A}_{1}^{\;}{A}_{2}^{\;}$与${A}_{3}^{\;}{A}_{4}^{\;}$间的距离为d,杆向上穿过磁场的过程中,由动能定理
$-mgd-\frac{1}{3}mgd+{W}_{安1}^{\;}=\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}m{v}_{0}^{2}$
杆过${A}_{3}^{\;}{A}_{4}^{\;}$后继续上升了nd,这一过程由动能定理
$-mgnd-\frac{1}{3}mgnd=0-\frac{1}{2}m{v}_{1}^{2}$
则:${W}_{安1}^{\;}=-\frac{(12n-4)}{3}mgd$
杆下落过程中${W}_{安2}^{\;}=-{F}_{2}^{\;}d=-\frac{2}{3}mgd$
由功能关系有${Q}_{1}^{\;}:{Q}_{2}^{\;}=|{W}_{安1}^{\;}|:|{W}_{安2}^{\;}|$
即:${Q}_{1}^{\;}:{Q}_{2}^{\;}=6n-2$
答:(1)金属杆CD向上,向下两次经过A3A4位置时的速度之比$\sqrt{2}:1$;
(2)金属杆CD向上运动经过A1A2刚进入磁场时的加速度大小$\frac{4+4\sqrt{2}}{3}g$;
(3)金属杆CD向上、向下两次经过磁场区域的过程中定值电阻R上产生的焦耳热之比(6n-2)
点评 本题是电磁感应与力学和能量等知识的综合应用,根据牛顿第二定律求加速度,以及结合运动学能够分析出金属棒的运动情况.考查分析和处理综合题的能力.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案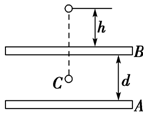 如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )
如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )| A. | 微粒下落过程中重力做功为mg(h+$\frac{d}{2}$),电场力做功为$\frac{qU}{2}$ | |
| B. | 微粒落入电场中,电势能逐渐增大,其增加量为$\frac{qU}{2}$ | |
| C. | 若微粒从距B板高2h处自由下落,则恰好能达到A板 | |
| D. | 微粒在下落过程中动能逐渐增加,重力势能逐渐减小 |
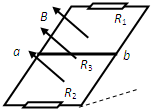 倾斜光滑、足够长的平行导轨处在匀强磁场中,导轨上的电阻R1=3Ω,下边接一最大电阻为6Ω的滑动变阻器R2,金属棒ab的质量为m、电阻R3=4Ω,其余电阻不计,斜面的斜角为α.则金属棒ab沿着导轨加速下滑的过程中( )
倾斜光滑、足够长的平行导轨处在匀强磁场中,导轨上的电阻R1=3Ω,下边接一最大电阻为6Ω的滑动变阻器R2,金属棒ab的质量为m、电阻R3=4Ω,其余电阻不计,斜面的斜角为α.则金属棒ab沿着导轨加速下滑的过程中( )| A. | 金属棒克服安培力做的功等于其机械能的减少量 | |
| B. | 重力和安培力对金属棒做功之和等于金属棒增加的动能、电路产生的热量之和 | |
| C. | 滑动变阻器接入电路的电阻越小,金属棒匀速运动时受到的安培力越大 | |
| D. | 改变滑动变阻器接入电路的电阻,当金属棒匀速运动后R1的电功率最大时,R1、R2、R3的功率之比为P1:P2:P3=2:1:6 |
| A. | 电源两极间的电压等于电源电动势 | |
| B. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 | |
| C. | 电源电动势的数值等于外电压之和 | |
| D. | 电源电动势与外电路的组成无关 |
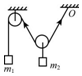
| A. | m1>$\frac{1}{2}$m2 | |
| B. | m1<$\frac{1}{2}$m2 | |
| C. | 若使m1的质量逐渐增加一些,整个装置一定能达到的平衡 | |
| D. | 若将右边绳子悬点O向右平移一些,则重物m2将会下降一些 |
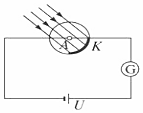 用频率未知的紫外线照射某光电管的阴极时,有光电子飞出.现给你一个电压可调且可指示电压数值的直流电源和一个灵敏度很高的灵敏电流计,试在图的方框中设计一种电路(光电管已画出),要求用该电路测量用所给紫外线照射光电管的阴极时产生的光电子的最大初动能.按照你设计的电路,重要的操作以及需要记录的数据是当加反向电压时,调节滑动触头P,使电流计的示数为零,记录此时电压表的示数U.你所测量的光电子的最大初动能是eU(已知电子电荷量为e).
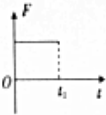
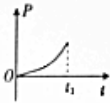
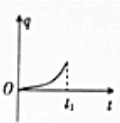
用频率未知的紫外线照射某光电管的阴极时,有光电子飞出.现给你一个电压可调且可指示电压数值的直流电源和一个灵敏度很高的灵敏电流计,试在图的方框中设计一种电路(光电管已画出),要求用该电路测量用所给紫外线照射光电管的阴极时产生的光电子的最大初动能.按照你设计的电路,重要的操作以及需要记录的数据是当加反向电压时,调节滑动触头P,使电流计的示数为零,记录此时电压表的示数U.你所测量的光电子的最大初动能是eU(已知电子电荷量为e). 如图所示,虚线右侧存在匀强磁场,磁场方向垂直纸面向外,具有一定电阻的正方形金属线框的右边与磁场的边界重合.在外力作用下,金属线框从O时刻由静止开始,以垂直于磁场边界的恒定加速度a进入磁场区域,t1时刻线框全部进入磁场.若规定顺时针方向为感应电流i的正方形,则感应电流i、外力大小为F,线框中电功率的瞬时值P以及通过导体横截面的电荷量q随时间变化的关系正确的是( )
如图所示,虚线右侧存在匀强磁场,磁场方向垂直纸面向外,具有一定电阻的正方形金属线框的右边与磁场的边界重合.在外力作用下,金属线框从O时刻由静止开始,以垂直于磁场边界的恒定加速度a进入磁场区域,t1时刻线框全部进入磁场.若规定顺时针方向为感应电流i的正方形,则感应电流i、外力大小为F,线框中电功率的瞬时值P以及通过导体横截面的电荷量q随时间变化的关系正确的是( )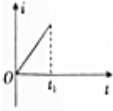
 粗细均匀的两端开口的U形细玻璃管开口向下竖直放置时,在左、右管中各有长度是L的水银柱封闭住总长是8L的气柱A,如图,左、右管之间的距离忽略不计,左、右管长度都是6L,两水银柱的下表面到管口距离相等.大气压保持为p=4ρgL,ρ是水银的密度,g是重力加速度.把一侧的管口封住(不计厚度),再缓慢转动U形管,使其开口向上竖直放置,两侧水银柱的长度不变.
粗细均匀的两端开口的U形细玻璃管开口向下竖直放置时,在左、右管中各有长度是L的水银柱封闭住总长是8L的气柱A,如图,左、右管之间的距离忽略不计,左、右管长度都是6L,两水银柱的下表面到管口距离相等.大气压保持为p=4ρgL,ρ是水银的密度,g是重力加速度.把一侧的管口封住(不计厚度),再缓慢转动U形管,使其开口向上竖直放置,两侧水银柱的长度不变.