��Ŀ����
1�� ��ͼ��ʾ�������Ҳ������ǿ�ų����ų�����ֱֽ�����⣬����һ������������ν����߿���ұ���ų��ı߽��غϣ������������£������߿��Oʱ���ɾ�ֹ��ʼ���Դ�ֱ�ڴų��߽�ĺ㶨���ٶ�a����ų�����t1ʱ���߿�ȫ������ų������涨˳ʱ�뷽��Ϊ��Ӧ����i�������Σ����Ӧ����i��������СΪF���߿��е繦�ʵ�˲ʱֵP�Լ�ͨ����������ĵ����q��ʱ��仯�Ĺ�ϵ��ȷ���ǣ�������
��ͼ��ʾ�������Ҳ������ǿ�ų����ų�����ֱֽ�����⣬����һ������������ν����߿���ұ���ų��ı߽��غϣ������������£������߿��Oʱ���ɾ�ֹ��ʼ���Դ�ֱ�ڴų��߽�ĺ㶨���ٶ�a����ų�����t1ʱ���߿�ȫ������ų������涨˳ʱ�뷽��Ϊ��Ӧ����i�������Σ����Ӧ����i��������СΪF���߿��е繦�ʵ�˲ʱֵP�Լ�ͨ����������ĵ����q��ʱ��仯�Ĺ�ϵ��ȷ���ǣ�������| A�� | 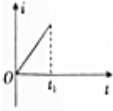 | B�� | 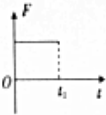 | C�� | 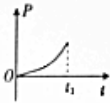 | D�� | 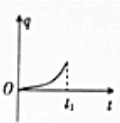 |
���� ���߿����ų����и�Ÿ��ߣ������˶�ѧ��ʽ��֪�ٶ���ʱ���ϵ���ɷ����ڵ�Ÿ�Ӧ����E=BLv���ɵó�������Ӧ�綯�����ٶȹ�ϵ���ɱպϵ�·ŷķ������ȷ����Ӧ�����Ĵ�С�����ɰ�������ʽ��ȷ�����С��ʱ��Ĺ�ϵ����ţ�ٵڶ�������ȷ��������ʱ��Ĺ�ϵ�����ó����������ʵı���ʽ���ֱ�ó�������ʱ��Ĺ�ϵ��
��� �⣺A���߿����ȼ����˶������ٶ�v=at����Ӧ�綯��E=BLv����Ӧ���� i=$\frac{E}{R}$=$\frac{BLat}{R}$��i��t�����ȣ���A��ȷ��
B���߿����ų��������ܵ��İ�����FB=BiL=$\frac{{B}^{2}{L}^{2}at}{R}$����ţ�ٵڶ����ɵã�F-FB=ma���� F=ma+$\frac{{B}^{2}{L}^{2}at}{R}$��F-tͼ���Dz���ԭ�����бֱ�ߣ���B����
C���߿��λ��x=$\frac{1}{2}$at2�������q=It��t=$\frac{\overline{E}}{R}��t$=$\frac{BLx}{R}$=$\frac{BLa{t}^{2}}{2R}$��t2����q-tͼ��Ӧ�ǿ������ϣ���ԭ��������ߣ���C��ȷ��
D���߿�ĵ繦�� P=i2R=$\frac{{B}^{2}{L}^{2}{a}^{2}{t}^{2}}{R}$��t2����D��ȷ��
��ѡ��ACD��
���� �������Ĺؼ������˶�ѧ��ʽ�����ɸ��Ա���ʽ�������Ƶ����Ӷ��ó������Ƿ���ȷ���Լ������и�����ĸ�Ӧ�綯��E=BLv��֪��LΪ��Ч���ȣ�

 ��ͼ��ʾ����Դ�綯��ΪE������Ϊr��������C������֮����һͨ����Ե�������ҵĴ���С�պϿ���S1��S2����·�ȶ�����������ֱ����ļн�Ϊ�ȣ������й�˵����ȷ���ǣ�������
��ͼ��ʾ����Դ�綯��ΪE������Ϊr��������C������֮����һͨ����Ե�������ҵĴ���С�պϿ���S1��S2����·�ȶ�����������ֱ����ļн�Ϊ�ȣ������й�˵����ȷ���ǣ�������| A�� | ʹ��ƬP1����˻�������ʱ���Ȳ��� | |
| B�� | ʹ��ƬP2���϶˻�������ʱ���ȼ�С | |
| C�� | �Ͽ�����S1��S2����C���������һЩ�������� | |
| D�� | �Ͽ�����S1��S2����C������������һЩ���ȼ�С |

 ���������ĸ߶���0.8m������ϵԭ�㶨�������ϣ����·���Ϊ���������������ͼ��ʾ��ͨ��������ȷ��ͼ��A��B�����꣮
���������ĸ߶���0.8m������ϵԭ�㶨�������ϣ����·���Ϊ���������������ͼ��ʾ��ͨ��������ȷ��ͼ��A��B�����꣮




 ��ͼ��һ�Ա���ֲڵ�ƽ�н��������ֱ�̶���ˮƽ�����ϣ����������Ե���������������һ��ֵ����R����A1A2��A3A4�������д�ֱ�ڹ��ƽ���������ǿ�ų���һˮƽ������CDͨ�������������ڹ���ϣ���ʹ������CD��ijһ���ٶ���ֱ�����˶��������ų������������������λ��A5A6��Ȼ����ص����棬�˺����˶�����֪������CD�������Ħ������С��Ϊ��������$\frac{1}{3}$����������C�����˶�����A1A2��A3A4λ��ʱ���ٶ�֮��Ϊ2��1��A3A4��A5A6��ľ�����A1A2��A3A4��ľ����n����������CD�����˶��ս���ų�������������˶����������ٶ�Ϊg����������������CD�ĵ��趼���Բ��ƣ���
��ͼ��һ�Ա���ֲڵ�ƽ�н��������ֱ�̶���ˮƽ�����ϣ����������Ե���������������һ��ֵ����R����A1A2��A3A4�������д�ֱ�ڹ��ƽ���������ǿ�ų���һˮƽ������CDͨ�������������ڹ���ϣ���ʹ������CD��ijһ���ٶ���ֱ�����˶��������ų������������������λ��A5A6��Ȼ����ص����棬�˺����˶�����֪������CD�������Ħ������С��Ϊ��������$\frac{1}{3}$����������C�����˶�����A1A2��A3A4λ��ʱ���ٶ�֮��Ϊ2��1��A3A4��A5A6��ľ�����A1A2��A3A4��ľ����n����������CD�����˶��ս���ų�������������˶����������ٶ�Ϊg����������������CD�ĵ��趼���Բ��ƣ���

