题目内容
3.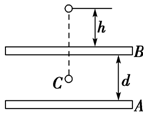 如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )
如图所示,带电平行金属板A、B,板间的电势差大小为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电荷量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B板的正中央C点,则( )| A. | 微粒下落过程中重力做功为mg(h+$\frac{d}{2}$),电场力做功为$\frac{qU}{2}$ | |
| B. | 微粒落入电场中,电势能逐渐增大,其增加量为$\frac{qU}{2}$ | |
| C. | 若微粒从距B板高2h处自由下落,则恰好能达到A板 | |
| D. | 微粒在下落过程中动能逐渐增加,重力势能逐渐减小 |
分析 微粒在下落过程中先做加速运动,后做减速运动,动能先增大,后减小.重力一直做正功,重力一直减小.微粒下落过程中重力做功为mg(h+$\frac{d}{2}$),电场力做功为-$\frac{1}{2}$qU.微粒落入电场中,电场力做负功,电势能逐渐增大,其增加量为$\frac{1}{2}$qU.根据动能定理研究微粒从距B板高2h处自由下落,能否到达A板.
解答 解:A、微粒下降的高度为h+$\frac{d}{2}$,重力做正功,为WG=mg(h+$\frac{d}{2}$),电场力向上,位移向下,电场力做负功,WE=-q$\frac{U}{2}$=-$\frac{1}{2}$qU.故A错误;
B、微粒落入电场中,克服电场力做功,电势能逐渐增大,其增加量等于克服电场力做的功,为$\frac{qU}{2}$,故B正确;
C、由题微粒恰能落至A,B板的正中央c点过程,由动能定理得:
mg(h+$\frac{d}{2}$)-$\frac{1}{2}$qU=0 ①,
若微粒从距B板高2h处自由下落,设达到A板的速度为v,则由动能定理得:
mg(2h+d)-qU=$\frac{1}{2}$mv2 ②,
由①②联立得v=0,即恰好能达到A板,故C正确;
D、微粒在下落过程中,进入电场前做自由落体运动,动能逐渐增加,重力势能逐渐减小;进入电场后是减速运动,动能减小;故D错误;
故选:BC
点评 本题根据动能定理研究微粒能否到达A板,也可以根据牛顿第二定律和运动学公式分析.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
13.如图是物体做直线运动的v-t图象,以下说法不正确的是( )


| A. | 第1 s内和第3 s内的运动方向相反 | |
| B. | 第3 s内和第4 s内的加速度相同 | |
| C. | 第1 s内和第4 s内的位移大小不相等 | |
| D. | 0~2 s和0~4 s内的平均速度大小相等 |
11. 如图所示,一斜面静止在水平地面上,位于斜面上的物块M在沿斜面向上的拉力F作用下处于静止状态.设斜面作用与物块的静摩擦力为f1,地面对斜面的摩擦力为f2,则下列叙述正确的是( )
如图所示,一斜面静止在水平地面上,位于斜面上的物块M在沿斜面向上的拉力F作用下处于静止状态.设斜面作用与物块的静摩擦力为f1,地面对斜面的摩擦力为f2,则下列叙述正确的是( )
 如图所示,一斜面静止在水平地面上,位于斜面上的物块M在沿斜面向上的拉力F作用下处于静止状态.设斜面作用与物块的静摩擦力为f1,地面对斜面的摩擦力为f2,则下列叙述正确的是( )
如图所示,一斜面静止在水平地面上,位于斜面上的物块M在沿斜面向上的拉力F作用下处于静止状态.设斜面作用与物块的静摩擦力为f1,地面对斜面的摩擦力为f2,则下列叙述正确的是( )| A. | f1方向可能沿斜面向下 | |
| B. | f1方向可能沿斜面向上 | |
| C. | 斜面对物体的作用力大小为Mg | |
| D. | 地面对斜面的摩擦力f2方向一定向左 |
18.如图为多用电表的内部结构图,开关s接____时,电表作为较小量程的电流表使用.( )


| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
5.如图,当一个条形磁铁N极靠近一个金属导体时,导体的表面出现了电流.下列说法 正确的是( )


| A. | 电流产生的磁场与磁铁磁场方向相同 | |
| B. | 从上往下看,电流的方向是顺时针的 | |
| C. | 磁铁停止运动,电流仍保持不变 | |
| D. | 导体中将产生热量并向外扩散 |
 在水平面上平行放置着两根长度均为L=5m的金属导轨MN和PQ,导轨间距为d=2m,导轨和电路的连接如图所示.在导轨的MP端放置着一根金属棒,与导舅垂直且接触良好.空间中存在竖直向上方向的匀强磁场,磁感应强度为B=1T.将开关S1闭合,S2断开,电压表和电流表的示数分别为U1=1V和I1=0.5A,金属棒仍处于静止状态;再将开关S2闭合,电流表的示数为I2=3.5A,金属棒在导轨上由静止开始运动,运动过程中金属棒始终与导轨垂直.设金属棒的质量为m=2kg,金属棒与导轨之间的动摩擦因数为μ=0.1.忽略导轨的电阻以及金属棒运动过程中产生的感应电动势,重力加速度为g=10m/s2.求:
在水平面上平行放置着两根长度均为L=5m的金属导轨MN和PQ,导轨间距为d=2m,导轨和电路的连接如图所示.在导轨的MP端放置着一根金属棒,与导舅垂直且接触良好.空间中存在竖直向上方向的匀强磁场,磁感应强度为B=1T.将开关S1闭合,S2断开,电压表和电流表的示数分别为U1=1V和I1=0.5A,金属棒仍处于静止状态;再将开关S2闭合,电流表的示数为I2=3.5A,金属棒在导轨上由静止开始运动,运动过程中金属棒始终与导轨垂直.设金属棒的质量为m=2kg,金属棒与导轨之间的动摩擦因数为μ=0.1.忽略导轨的电阻以及金属棒运动过程中产生的感应电动势,重力加速度为g=10m/s2.求: 如图长为L的很细的绝缘杆均匀带有正电荷,电荷在杆子内部左方$\frac{L}{4}$处的A点产生的场强为E1,在杆外部右方$\frac{L}{4}$的B点产生的场强为E2,若将杆子由中间截断,并将右段叠在左段上,则此时A处的场强为0,B处的场强为$2({E}_{2}^{\;}-{E}_{1}^{\;})$.
如图长为L的很细的绝缘杆均匀带有正电荷,电荷在杆子内部左方$\frac{L}{4}$处的A点产生的场强为E1,在杆外部右方$\frac{L}{4}$的B点产生的场强为E2,若将杆子由中间截断,并将右段叠在左段上,则此时A处的场强为0,B处的场强为$2({E}_{2}^{\;}-{E}_{1}^{\;})$. 如图,一对表面粗糙的平行金属轨道竖直固定在水平地面上,轨道与地面绝缘,轨道顶端连接有一定值电阻R,在A1A2、A3A4区域内有垂直于轨道平面向里的匀强磁场,一水平金属杆CD通过两金属环套在轨道上,现使金属杆CD以某一初速度竖直向上运动,穿过磁场区域后继续上升到最高位置A5A6,然后落回到地面,此后不再运动,已知金属杆CD与轨道间的摩擦力大小恒为其重力的$\frac{1}{3}$倍,金属杆C向上运动经过A1A2和A3A4位置时,速度之比为2:1,A3A4与A5A6间的距离是A1A2与A3A4间的距离的n倍,金属杆CD向下运动刚进入磁场区域就做匀速运动,重力加速度为g,金属轨道与金属杆CD的电阻都忽略不计.求:
如图,一对表面粗糙的平行金属轨道竖直固定在水平地面上,轨道与地面绝缘,轨道顶端连接有一定值电阻R,在A1A2、A3A4区域内有垂直于轨道平面向里的匀强磁场,一水平金属杆CD通过两金属环套在轨道上,现使金属杆CD以某一初速度竖直向上运动,穿过磁场区域后继续上升到最高位置A5A6,然后落回到地面,此后不再运动,已知金属杆CD与轨道间的摩擦力大小恒为其重力的$\frac{1}{3}$倍,金属杆C向上运动经过A1A2和A3A4位置时,速度之比为2:1,A3A4与A5A6间的距离是A1A2与A3A4间的距离的n倍,金属杆CD向下运动刚进入磁场区域就做匀速运动,重力加速度为g,金属轨道与金属杆CD的电阻都忽略不计.求: