题目内容
4.一单匝闭合线圈绕垂直磁场的轴在匀强磁场中做匀速转动,线圈转速为240r/min,当线圈平面转动至与磁场平行时,线圈的电动势为2.0V.则线圈在转动过程中磁通量的最大值为$\frac{1}{2π}$V,转动过程中产生的电动势最大值为2V,设线圈从垂直磁场瞬时开始计时,该线圈电动势的瞬时表达式e=2.0sin4πt(V),1s末的电动势瞬时值为0V.分析 由转速来确定角速度,再结合感应电动势最大值Em=BSω,及感应电动势,即可求解磁通量的最大值.
当线圈平面转至与磁场方向平行时,产生的感应电动势最大,结合峰值,得出从中性面开始计时电动势的瞬时表达式,从而求出t=1s时线圈的电动势.
解答 解:线圈转速为n=240r/min=4r/s,那么角速度ω=2πn=4πrad/s;
当线圈平面转至与磁场方向平行时,产生的感应电动势最大,
则Em=2.0V,ω=4πrad/s,
由感应电动势最大值Em=BSω,解得:磁通量的最大值为BS=$\frac{2}{4π}$V=$\frac{1}{2π}$V;
则瞬时表达式e=Emsinωt=2.0sin4πt(V).
当在t=1s时,e=2.0×sin4π=0V.
故答案为:$\frac{1}{2π}$V,2V,e=2.0sin4πt(V);0.
点评 解决本题的关键掌握感应电动势的瞬时表达式,知道线圈平面与磁场平行时,产生的感应电动势最大.

练习册系列答案
相关题目
19.当一段直导体棒在匀强磁场中,匀速切割磁感线运动时( )
| A. | 一定产生感应电流 | B. | 一定产生焦耳热 | ||
| C. | 一定受到磁场力作用 | D. | 一定产生感应电动势 |
9.如图所示,是一质点作直线运动的v-t图象,下列说法中正确的是( )


| A. | 整个过程中,18-22秒段的加速度数值最大 | |
| B. | 整个过程中,14-18秒段的加速度数值最大 | |
| C. | 整个过程中,20s时质点离出发点最远 | |
| D. | 14-18秒段所表示的运动通过的路程是34m |
13.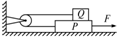 如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )
如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )
 如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )
如图所示,物体Q重40N,物体P重80N,A与B、A与地面间的最大静摩擦力均为μ.滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F=50N拉P使它做匀速运动,则μ大小为( )| A. | $\frac{1}{4}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{16}$ | D. | $\frac{1}{5}$ |
14.竖直上抛运动的物体,到达最高点时( )
| A. | 具有向上的速度和向下加速度 | B. | 速度为零,加速度向下 | ||
| C. | 速度为零,加速度向上 | D. | 具有向下的速度和向下加速度 |
 如图所示,两个带有等量同种电荷的小球,质量均为m,用长L的丝线挂在同一点,平衡时丝线与竖直方向成α角,则每个小球受到的静电力为mgtanα,小球的带电量为$2Lsinα\sqrt{\frac{mgtanα}{k}}$.
如图所示,两个带有等量同种电荷的小球,质量均为m,用长L的丝线挂在同一点,平衡时丝线与竖直方向成α角,则每个小球受到的静电力为mgtanα,小球的带电量为$2Lsinα\sqrt{\frac{mgtanα}{k}}$. 如图所示,质量M=4kg、长L=3m的长木板放置于光滑的水平地面上,其左端有一大小可以忽略,质量为m=1kg的物块,物块和木板间的动摩擦因数为0.2.开始时物块和木板都处于静止状态,现在对物块施加F=4N,方向水平向右的恒定拉力,求:
如图所示,质量M=4kg、长L=3m的长木板放置于光滑的水平地面上,其左端有一大小可以忽略,质量为m=1kg的物块,物块和木板间的动摩擦因数为0.2.开始时物块和木板都处于静止状态,现在对物块施加F=4N,方向水平向右的恒定拉力,求: