题目内容
5. 人造地球卫星P绕地球球心作匀速圆周运动,已知P卫星的质量为m,距地球球心的距离为r,地球的质量为M,引力恒量为G,求:
人造地球卫星P绕地球球心作匀速圆周运动,已知P卫星的质量为m,距地球球心的距离为r,地球的质量为M,引力恒量为G,求:(1)卫星P与地球间的万有引力;
(2)卫星P的运动周期;
(3)现有另一地球卫星Q,Q绕地球运行的周期是卫星P绕地球运行周期的8倍,且P、Q的运行轨迹位于同一平面内,如图所示,求卫星P、Q在绕地球运行过程中,两星间相距最近时的距离多大.
分析 (1)根据万有引力定律的公式求出卫星P与地球间的万有引力大小.
(2)根据万有引力提供向心力求出卫星P的运动周期.
(3)当P、Q、地球共线时,且位移地球同一侧相距最近.
解答 解:(1)卫星P与地球间的万有引力F=$\frac{GMm}{{r}^{2}}$;
(2)根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,卫星P的运动周期T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$;
(3)卫星Q的周期是卫星P周期的8倍,根据T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$知,卫星Q的轨道半径是卫星P轨道半径的4倍,即r′=4r,
当 P、Q、地球共线且P、Q位于地球同侧时最近,最近距离d=4r-r=3r.
答:(1)卫星P与地球间的万有引力为$\frac{GMm}{{r}^{2}}$;
(2)卫星P的运动周期为$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$;
(3)卫星P、Q在绕地球运行过程中,两星间相距最近时的距离为3r.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道周期与轨道半径的关系,基础题.

练习册系列答案
相关题目
13.某人造卫星绕地球做匀速圆周运动,其轨道半径为r,设地球半径为R,地面的重力加速度为g,万有引力常为G,根据以上信息不能求出的物理量的是( )
| A. | 卫星受到地球的万有引力 | B. | 地球的质量 | ||
| C. | 卫星的周期 | D. | 卫星的加速度 |
10.如图所示,R1=6Ω,R2=3Ω,R3=4Ω,接入电路后,关于这三只电阻的判断正确的是( ) 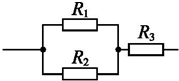

| A. | 电流之比I1:I2:I3=1:2:3 | B. | 电压之比U1:U2:U3=2:2:1 | ||
| C. | 功率之比P1:P2:P3=1:2:6 | D. | 功率之比P1:P2:P3=6:3:4 |
17.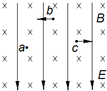 如图所示,匀强电场E竖直向下,匀强磁场B垂直纸面向里.现有三个带有等量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做匀速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )
如图所示,匀强电场E竖直向下,匀强磁场B垂直纸面向里.现有三个带有等量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做匀速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )
 如图所示,匀强电场E竖直向下,匀强磁场B垂直纸面向里.现有三个带有等量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做匀速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )
如图所示,匀强电场E竖直向下,匀强磁场B垂直纸面向里.现有三个带有等量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做匀速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )| A. | 三个油滴都带正电 | |
| B. | 油滴a一定是做顺时针方向的圆周运动 | |
| C. | 三个油滴中b的质量最大 | |
| D. | 三个油滴中c的质量最大 |
14.下列物理量中都属于矢量的是( )
| A. | 力、加速度 | B. | 时间、质量 | C. | 位移、速率 | D. | 加速度、温度 |
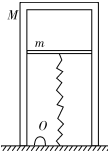 一汽缸竖直放在水平地面上,缸体质量M=10kg,活塞质量m=4kg,活塞横截面积S=2×10-3m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面有气孔O与外界相通,大气压强P0=1.0×105Pa;活塞下面与劲度系数k=2×103M/m的轻弹簧相连;当汽缸内气体温度为127℃时弹簧为自然长度,此时缸内气柱长度L1=20cm,g取10m/s2,缸体始终竖直,活塞不漏气且与缸壁无摩擦.
一汽缸竖直放在水平地面上,缸体质量M=10kg,活塞质量m=4kg,活塞横截面积S=2×10-3m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面有气孔O与外界相通,大气压强P0=1.0×105Pa;活塞下面与劲度系数k=2×103M/m的轻弹簧相连;当汽缸内气体温度为127℃时弹簧为自然长度,此时缸内气柱长度L1=20cm,g取10m/s2,缸体始终竖直,活塞不漏气且与缸壁无摩擦.