题目内容
如图所示,一小球从斜轨道的某高度处自由滑下,然后沿竖直圆轨道的内侧运动.已知圆轨道的半径为R,重力加速度为g.(1)要使小球能通过圆轨道的最高点,小球在圆轨道最高点时的速度至少为多大?
(2)如果忽略摩擦阻力,要使小球能通过圆轨道的最高点,小球的初位置必须比圆轨道最低点高出多少?
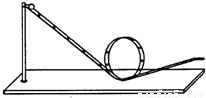
【答案】分析:使小球能够通过圆轨道最高点,那么小球在最高点时应该是恰好是物体的重力作为物体的向心力,由向心力的公式可以求得此时的最小的速度,再由机械能守恒可以求得离最低点的高度h.
解答:解:(1)在圆轨道的最高点,由牛顿第二定律有:mg=m
得:v=
要使小球能通过圆轨道的最高点,小球在轨道最高点时的速度至少为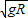
(2)设小球的初位置比圆轨道最低点高出h时,小球刚好能通过圆轨道最高点,由机械能守恒定律有:
mg(h-2R)=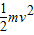
解得:h=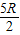
答:(1)要使小球能通过圆轨道的最高点,小球在圆轨道最高点时的速度至少为 ;
;
(2)如果忽略摩擦阻力,要使小球能通过圆轨道的最高点,小球的初位置必须比圆轨道最低点高出
点评:本题属于圆周运动中绳的模型,在最高点时应该是重力恰好做为圆周运动的向心力,对于圆周运动中的两种模型一定要牢牢的掌握住.
解答:解:(1)在圆轨道的最高点,由牛顿第二定律有:mg=m

得:v=

要使小球能通过圆轨道的最高点,小球在轨道最高点时的速度至少为
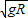
(2)设小球的初位置比圆轨道最低点高出h时,小球刚好能通过圆轨道最高点,由机械能守恒定律有:
mg(h-2R)=
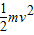
解得:h=
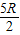
答:(1)要使小球能通过圆轨道的最高点,小球在圆轨道最高点时的速度至少为
 ;
;(2)如果忽略摩擦阻力,要使小球能通过圆轨道的最高点,小球的初位置必须比圆轨道最低点高出

点评:本题属于圆周运动中绳的模型,在最高点时应该是重力恰好做为圆周运动的向心力,对于圆周运动中的两种模型一定要牢牢的掌握住.

练习册系列答案
相关题目
 如图所示,一小球从斜轨道的某高度处由静止滑下,然后沿竖直光滑轨道的内侧运动.已知圆轨道的半径为R,忽略一切摩擦阻力.则下列说法正确的是( )
如图所示,一小球从斜轨道的某高度处由静止滑下,然后沿竖直光滑轨道的内侧运动.已知圆轨道的半径为R,忽略一切摩擦阻力.则下列说法正确的是( )| A、在轨道最低点、最高点,轨道对小球作用力的方向是相同的 | B、小球的初位置比圆轨道最低点高出2R时,小球能通过圆轨道的最高点 | C、小球的初位置比圆轨道最低点高出0.5R时,小球在运动过程中能不脱离轨道 | D、小球的初位置只有比圆轨道最低点高出2.5R时,小球在运动过程中才能不脱离轨道 |
 如图所示,一小球从斜轨道的某高度处自由滑下,然后沿竖直圆轨道的内侧运动.已知圆轨道的半径为R,重力加速度为g.
如图所示,一小球从斜轨道的某高度处自由滑下,然后沿竖直圆轨道的内侧运动.已知圆轨道的半径为R,重力加速度为g. 如图所示,一小球从斜轨道的某高度下滑,然后沿竖直圆轨道的内侧运动.已知圆轨道的半径为R,重力加速度为g.
如图所示,一小球从斜轨道的某高度下滑,然后沿竖直圆轨道的内侧运动.已知圆轨道的半径为R,重力加速度为g. 如图所示,一小球从斜轨道的某高度处自由滑下,然后沿竖直圆轨道的内侧运动.已知圆轨道的半径为R,重力加速度为g.如果忽略阻力,要使小球能够通过圆轨道的最高点,且轨道对小球的压力不超过小球重力的3倍,小球的初位置相对于圆形轨道底部的高度H的取值范围是多大?
如图所示,一小球从斜轨道的某高度处自由滑下,然后沿竖直圆轨道的内侧运动.已知圆轨道的半径为R,重力加速度为g.如果忽略阻力,要使小球能够通过圆轨道的最高点,且轨道对小球的压力不超过小球重力的3倍,小球的初位置相对于圆形轨道底部的高度H的取值范围是多大?