题目内容
1.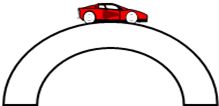 如图所示,质量为1t的汽车以10m/s的速度通过半径R=40m的拱桥桥顶时,车对桥顶的压力是多少?为使汽车能安全通过桥顶(汽车不脱离桥面),汽车驶上桥顶时速度不得超过多少?
如图所示,质量为1t的汽车以10m/s的速度通过半径R=40m的拱桥桥顶时,车对桥顶的压力是多少?为使汽车能安全通过桥顶(汽车不脱离桥面),汽车驶上桥顶时速度不得超过多少?
分析 (1)汽车经过拱桥最高点时,由重力和桥面的支持力的合力提供向心力,根据向心力公式和牛顿第二、第三定律可列式求解;
(2)若要使汽车到达桥顶不脱离桥面,汽车对桥恰好无压力,重力完全提供汽车的向心力,根据向心力公式和牛顿第二定律可列式求解
解答 解:当车行驶至桥顶时,据牛顿运动定律得:
$mg-{F}_{N}=m\frac{{v}^{2}}{R}$
解得:${F_N}=m(g-\frac{v^2}{R})=7.5×{10^3}N$
据牛顿第三定律,车对桥面压力为:
${F_N}'={F_N}=7.5×{10^3}N$
为使汽车不脱离桥面,则有:
$mg=m\frac{{v{'^2}}}{R}$
解得:v=20m/s
答:车对桥顶的压力是7.5×103N,为使汽车能安全通过桥顶(汽车不脱离桥面),汽车驶上桥顶时速度不得超过20m/s.
点评 本题关键找出车经过桥的最高点时的向心力来源,然后根据牛顿第二定律和向心力公式列式进行求解

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11. 卡拉OK用的话筒,内有将声音信号转换为电信号的传感器.其中有一种是动圈式的,如图所示.在弹性膜片后面粘接一个轻小的金属线圈,线圈处于永磁体的磁场中.声波使膜片振动时,就会将声音信号转变为电信号.下列说法正确的是( )
卡拉OK用的话筒,内有将声音信号转换为电信号的传感器.其中有一种是动圈式的,如图所示.在弹性膜片后面粘接一个轻小的金属线圈,线圈处于永磁体的磁场中.声波使膜片振动时,就会将声音信号转变为电信号.下列说法正确的是( )
 卡拉OK用的话筒,内有将声音信号转换为电信号的传感器.其中有一种是动圈式的,如图所示.在弹性膜片后面粘接一个轻小的金属线圈,线圈处于永磁体的磁场中.声波使膜片振动时,就会将声音信号转变为电信号.下列说法正确的是( )
卡拉OK用的话筒,内有将声音信号转换为电信号的传感器.其中有一种是动圈式的,如图所示.在弹性膜片后面粘接一个轻小的金属线圈,线圈处于永磁体的磁场中.声波使膜片振动时,就会将声音信号转变为电信号.下列说法正确的是( )| A. | 该传感器是根据电流的磁效应工作的 | |
| B. | 该传感器是根据电磁感应原理工作的 | |
| C. | 膜片振动时线圈中产生动生电动势 | |
| D. | 膜片振动时线圈中产生感生电动势 |
16. 质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s.下列说法正确的是( )
质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s.下列说法正确的是( )
 质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s.下列说法正确的是( )
质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s.下列说法正确的是( )| A. | 小车重力所做的功是mgh | B. | 合力对小车做的功是$\frac{m{v}^{2}}{2}$+mgh | ||
| C. | 阻力对小车做的功是$\frac{m{v}^{2}}{2}$+mgh-Fs | D. | 推力对小车做的功是Fs-mgh |
6. 在第15届机器人世界杯赛上,中科大“蓝鹰”队获得仿真2D组冠军和服务机器人组亚军.如图所示,科大著名服务机器人“可佳”要执行一项任务,给它设定了如下动作程序:在平面内由点(0,0)出发,沿直线运动到点(3,1),再由点(3,1)沿直线运动到点(1,4),又由点(1,4)沿直线运动到点(5,5),然后由点(5,5)沿直线运动到点(2,2).该个过程中机器人所用时间是2$\sqrt{2}$s,则( )
在第15届机器人世界杯赛上,中科大“蓝鹰”队获得仿真2D组冠军和服务机器人组亚军.如图所示,科大著名服务机器人“可佳”要执行一项任务,给它设定了如下动作程序:在平面内由点(0,0)出发,沿直线运动到点(3,1),再由点(3,1)沿直线运动到点(1,4),又由点(1,4)沿直线运动到点(5,5),然后由点(5,5)沿直线运动到点(2,2).该个过程中机器人所用时间是2$\sqrt{2}$s,则( )
 在第15届机器人世界杯赛上,中科大“蓝鹰”队获得仿真2D组冠军和服务机器人组亚军.如图所示,科大著名服务机器人“可佳”要执行一项任务,给它设定了如下动作程序:在平面内由点(0,0)出发,沿直线运动到点(3,1),再由点(3,1)沿直线运动到点(1,4),又由点(1,4)沿直线运动到点(5,5),然后由点(5,5)沿直线运动到点(2,2).该个过程中机器人所用时间是2$\sqrt{2}$s,则( )
在第15届机器人世界杯赛上,中科大“蓝鹰”队获得仿真2D组冠军和服务机器人组亚军.如图所示,科大著名服务机器人“可佳”要执行一项任务,给它设定了如下动作程序:在平面内由点(0,0)出发,沿直线运动到点(3,1),再由点(3,1)沿直线运动到点(1,4),又由点(1,4)沿直线运动到点(5,5),然后由点(5,5)沿直线运动到点(2,2).该个过程中机器人所用时间是2$\sqrt{2}$s,则( )| A. | 机器人的运动轨迹是一条直线 | |
| B. | 机器人不会两次通过同一点 | |
| C. | 整个过程中机器人的位移大小为$\sqrt{2}$m | |
| D. | 整个过程中机器人的平均速度为1.0m/s |
13. 某运动员在110米跨栏时采用蹲踞式起跑,发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设质量为m的运动员,在起跑时前进的距离x内,重心上升高度为h,获得的速度为v,克服阻力做功为W阻,则在此过程中,下列说法中正确的是( )
某运动员在110米跨栏时采用蹲踞式起跑,发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设质量为m的运动员,在起跑时前进的距离x内,重心上升高度为h,获得的速度为v,克服阻力做功为W阻,则在此过程中,下列说法中正确的是( )
 某运动员在110米跨栏时采用蹲踞式起跑,发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设质量为m的运动员,在起跑时前进的距离x内,重心上升高度为h,获得的速度为v,克服阻力做功为W阻,则在此过程中,下列说法中正确的是( )
某运动员在110米跨栏时采用蹲踞式起跑,发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设质量为m的运动员,在起跑时前进的距离x内,重心上升高度为h,获得的速度为v,克服阻力做功为W阻,则在此过程中,下列说法中正确的是( )| A. | 运动员的重力做功为W重=mgh | B. | 运动员机械能增量为$\frac{1}{2}$mv2+mgh | ||
| C. | 运动员的动能增加量W阻+mgh | D. | 运动员自身做功为$\frac{1}{2}$mv2+mgh-W阻 |
 如图所示,一圆柱形容器内,盛有很深的某种液体,其密度为水银的$\frac{1}{4}$,在容器的上方有一活塞,活塞与液面之间有L0=10cm高的密封气体,气体压强为1atm,一只管口向下的小试管竖直插入液体中,平衡时试管内外液面高度差h=4cm,试管密闭端到容器内液面的高度L=4cm,今向下缓慢移动活塞,试管将向下移动,整个过程温度不变,为使试管不沉到容器底部,活塞下移的距离不得超过多少?(不计容器内液面的变化)
如图所示,一圆柱形容器内,盛有很深的某种液体,其密度为水银的$\frac{1}{4}$,在容器的上方有一活塞,活塞与液面之间有L0=10cm高的密封气体,气体压强为1atm,一只管口向下的小试管竖直插入液体中,平衡时试管内外液面高度差h=4cm,试管密闭端到容器内液面的高度L=4cm,今向下缓慢移动活塞,试管将向下移动,整个过程温度不变,为使试管不沉到容器底部,活塞下移的距离不得超过多少?(不计容器内液面的变化)
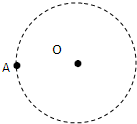 如图所示为恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,A行星的运行轨道半径为R0、周期为T0.
如图所示为恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,A行星的运行轨道半径为R0、周期为T0.