题目内容
12. 如图所示,ABCD是边长为L的正方形,在其中的适当区域内有匀强磁场,磁场方向垂直纸面向里.质量为m、电荷量为q的粒子以大小为v的速度垂直BC边从C点射入正方形区域,所经过的区域都有磁场,最后从A点射出磁场.不计粒子重力.求:
如图所示,ABCD是边长为L的正方形,在其中的适当区域内有匀强磁场,磁场方向垂直纸面向里.质量为m、电荷量为q的粒子以大小为v的速度垂直BC边从C点射入正方形区域,所经过的区域都有磁场,最后从A点射出磁场.不计粒子重力.求:(1)匀强磁场的磁感应强度B的大小?
(2)若完全相同的粒子以相同的速度从BC的中点O垂直BC边射入正方形区域,在到达P点前,所经过的区域没有磁场,从P点开始,所经过的区域都有磁场,最后从A点射出磁场.则P点到BC边的距离x=?
分析 粒子进入磁场中.由洛伦兹力提供向心力,由牛顿第二定律得到半径公式r=$\frac{mv}{qB}$,求出从A点射出时的磁感应强度;从O点射入时,画出轨迹根据几何关系求出x.
解答 解:(1)粒子从C点射入,从A点射出,所以轨迹是$\frac{1}{4}$的圆周,半径r=L,粒子在磁场中洛伦兹力提供向心力,得:
$qvB=\frac{m{v}^{2}}{r}$
所以:$B=\frac{mv}{qr}=\frac{mv}{qL}$
(2)在到达P点前,所经过的区域没有磁场,从P点开始,所经过的区域都有磁场,最后从A点射出磁场,其运动的轨迹如图所示,
由几何关系可得:${r}^{2}=(r-\frac{1}{2}L)^{2}+(L-x)^{2}$
联立以上各式得:${x}^{2}-2Lx+\frac{1}{4}{L}^{2}=0$
得:$x=L-\frac{\sqrt{3}}{2}L$
答:(1)匀强磁场的磁感应强度B的大小是$\frac{mv}{qL}$;
(2)若完全相同的粒子以相同的速度从BC的中点O垂直BC边射入正方形区域,在到达P点前,所经过的区域没有磁场,从P点开始,所经过的区域都有磁场,最后从A点射出磁场.则P点到BC边的距离是(1-$\frac{\sqrt{3}}{2}$)L
点评 带电粒子在磁场中运动的类型,确定向心力来源,画出轨迹,运用牛顿第二定律列式是惯用的解题思路.平时要加强训练,才能运用自如.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.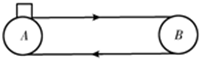 如图所示,水平传送带A、B两端点相距x=3.5m,以v0=2m/s的速度(始终保持不变)顺时针运转.今将一小煤块(可视为质点)无初速度地轻放在A点处,已知小煤块与传送带间的动摩擦因数为0.4.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕.小煤块从A运动到B的过程中( )
如图所示,水平传送带A、B两端点相距x=3.5m,以v0=2m/s的速度(始终保持不变)顺时针运转.今将一小煤块(可视为质点)无初速度地轻放在A点处,已知小煤块与传送带间的动摩擦因数为0.4.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕.小煤块从A运动到B的过程中( )
 如图所示,水平传送带A、B两端点相距x=3.5m,以v0=2m/s的速度(始终保持不变)顺时针运转.今将一小煤块(可视为质点)无初速度地轻放在A点处,已知小煤块与传送带间的动摩擦因数为0.4.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕.小煤块从A运动到B的过程中( )
如图所示,水平传送带A、B两端点相距x=3.5m,以v0=2m/s的速度(始终保持不变)顺时针运转.今将一小煤块(可视为质点)无初速度地轻放在A点处,已知小煤块与传送带间的动摩擦因数为0.4.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕.小煤块从A运动到B的过程中( )| A. | 煤块用了1s赶上皮带的速度 | |
| B. | 煤块从A处到B处所用的时间是2s | |
| C. | 划痕长度是4m | |
| D. | 煤块在静摩擦力作用下先做匀加速直线运动,再做匀速运动 |
3.三个完全相同的小球a、b、c,以相同的速度在光滑水面上分别与另外三个不同的静止小球相撞后,小球a被反向弹回,小球b与被碰球粘合在一起仍沿原方向运动,小球c恰好静止.比较这三种情况,以下说法中正确的是( )
| A. | a球获得的冲量最大 | |
| B. | b球损失的动能最多 | |
| C. | c球克服阻力做的功最多 | |
| D. | 三种碰撞过程,系统动量都是守恒的 |
20.一人从20m高的楼顶以10m/s的速度抛出一个质量为1kg的小球,小球落地速度为20m/s,g=10m/s2,则( )
①此人做功为50J
②此人做功为100J
③空气阻力做功为-100J
④小球克服空气阻力做功为50J.
①此人做功为50J
②此人做功为100J
③空气阻力做功为-100J
④小球克服空气阻力做功为50J.
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
17. 静电透镜是利用静电场使电子束会聚或发散的一种装置.如图所示为该透镜工作原理示意图,虚线表示这个静电场在xOy平面内的一簇等势线,等势线形状关于Ox轴、Oy轴对称,相邻两等势线间的电势差相等.图中实线为某个电子通过电场区域时的运动轨迹,电子从a点运动到b点过程( )
静电透镜是利用静电场使电子束会聚或发散的一种装置.如图所示为该透镜工作原理示意图,虚线表示这个静电场在xOy平面内的一簇等势线,等势线形状关于Ox轴、Oy轴对称,相邻两等势线间的电势差相等.图中实线为某个电子通过电场区域时的运动轨迹,电子从a点运动到b点过程( )
 静电透镜是利用静电场使电子束会聚或发散的一种装置.如图所示为该透镜工作原理示意图,虚线表示这个静电场在xOy平面内的一簇等势线,等势线形状关于Ox轴、Oy轴对称,相邻两等势线间的电势差相等.图中实线为某个电子通过电场区域时的运动轨迹,电子从a点运动到b点过程( )
静电透镜是利用静电场使电子束会聚或发散的一种装置.如图所示为该透镜工作原理示意图,虚线表示这个静电场在xOy平面内的一簇等势线,等势线形状关于Ox轴、Oy轴对称,相邻两等势线间的电势差相等.图中实线为某个电子通过电场区域时的运动轨迹,电子从a点运动到b点过程( )| A. | a点的电势高于b点的电势 | |
| B. | 电子在a点的加速度大于在b点的加速度 | |
| C. | 电子在a点的动能大于在b点的动能 | |
| D. | 电子在a点的电势能大于在b点的电势能 |
1. 随着中国电信业的发展,国产手机在手机市场上已经占有了相当大的市场份额.如图所示是中国科健股份有限公司生产的一块手机电池外壳上的文字说明,由此可知此电池的电动势和待机状态下工作电流分别是C( )
随着中国电信业的发展,国产手机在手机市场上已经占有了相当大的市场份额.如图所示是中国科健股份有限公司生产的一块手机电池外壳上的文字说明,由此可知此电池的电动势和待机状态下工作电流分别是C( )
 随着中国电信业的发展,国产手机在手机市场上已经占有了相当大的市场份额.如图所示是中国科健股份有限公司生产的一块手机电池外壳上的文字说明,由此可知此电池的电动势和待机状态下工作电流分别是C( )
随着中国电信业的发展,国产手机在手机市场上已经占有了相当大的市场份额.如图所示是中国科健股份有限公司生产的一块手机电池外壳上的文字说明,由此可知此电池的电动势和待机状态下工作电流分别是C( )| A. | 4.2V 14.58mA | B. | 4.2V 700mA | C. | 3.7V 700mA | D. | 3.7V 14.58mA |
2. 如图所示,A、B是两个相同的轻弹簧,原长都是L0=10cm,劲度系数k=500N/m.若图中悬挂的两重物质量均为m,现测得两个弹簧的总长为26cm,则(g取10m/s2)( )
如图所示,A、B是两个相同的轻弹簧,原长都是L0=10cm,劲度系数k=500N/m.若图中悬挂的两重物质量均为m,现测得两个弹簧的总长为26cm,则(g取10m/s2)( )
 如图所示,A、B是两个相同的轻弹簧,原长都是L0=10cm,劲度系数k=500N/m.若图中悬挂的两重物质量均为m,现测得两个弹簧的总长为26cm,则(g取10m/s2)( )
如图所示,A、B是两个相同的轻弹簧,原长都是L0=10cm,劲度系数k=500N/m.若图中悬挂的两重物质量均为m,现测得两个弹簧的总长为26cm,则(g取10m/s2)( )| A. | m=3kg | B. | m=2kg | C. | m=1.5kg | D. | m=1kg |
 如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向.在x轴上方空间的第一、第二和第四象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xoy平面(纸面)向里的匀强磁场.一质量为m、电荷量为q的带电质点,从y轴上y=h处P1点以一定的水平初速度沿x轴负方向进入第二象限.然后经过x轴上x=2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动.之后经过y轴上y=-2h处的P3点进入第四象限.已知重力加速度为g.求:
如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向.在x轴上方空间的第一、第二和第四象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xoy平面(纸面)向里的匀强磁场.一质量为m、电荷量为q的带电质点,从y轴上y=h处P1点以一定的水平初速度沿x轴负方向进入第二象限.然后经过x轴上x=2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动.之后经过y轴上y=-2h处的P3点进入第四象限.已知重力加速度为g.求: