题目内容
7. 如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )| A. | b、c向心加速度相等,且大于a的向心加速度 | |
| B. | b所需向心力最大 | |
| C. | b、c的线速度大小相等,且大于a的线速度 | |
| D. | b、c周期相等,且大于a的周期 |
分析 根据万有引力提供向心力,得出向心加速度、线速度、周期与轨道半径的关系式,从而比较出大小.
解答 解:根据万有引力提供向心力,有 G$\frac{Mm}{{r}^{2}}$=ma=m$\frac{{v}^{2}}{r}$=m$\frac{4{π}^{2}}{{T}^{2}}$r,得 a=$\frac{GM}{{r}^{2}}$,v=$\sqrt{\frac{GM}{r}}$,T=2π$\sqrt{\frac{{r}^{3}}{GM}}$
A、根据a=$\frac{GM}{{r}^{2}}$,可知,卫星的轨道半径越大,加速度越小,所以b、c的向心加速度相等,小于a的向心加速度.故A错误.
B、由F=G$\frac{Mm}{{r}^{2}}$,可知:a、b质量相同,且小于c的质量,而b、c半径相同大于a的半径,所以Fa>Fb,Fc>Fb,可知b所需向心力最小.故B错误.
C、根据v=$\sqrt{\frac{GM}{r}}$,可知,卫星的轨道半径越大,线速度越小,所以b、c的线速度大小相等,小于a的线速度.故C错误.
D、根据T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,可知,卫星的轨道半径越大,周期越大.所以b、c的周期相同,大于a的周期.故D正确.
故选:D
点评 本题是要关键抓住万有引力提供向心力,先列式求解出线速度、周期和加速度的表达式,再进行讨论.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 光电效应和康普顿效应揭示了光的粒子性,都表明光子既有能量又有动量 | |
| B. | 一定量气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度降低而减少 | |
| C. | 折断的粉笔不能粘合在一起是因为受分子斥力的作用 | |
| D. | 组成原子核的核子的总质量大于该原子核的质量,这个现象是质量亏损 |
15. 如图所示为某质点在0-t2时间内的位移-时间(x-t)图象,图线为开口向下的抛物线,图中所标的量均已知.关于该质点在0-t2时间内的运动,下列说法正确的是( )
如图所示为某质点在0-t2时间内的位移-时间(x-t)图象,图线为开口向下的抛物线,图中所标的量均已知.关于该质点在0-t2时间内的运动,下列说法正确的是( )
 如图所示为某质点在0-t2时间内的位移-时间(x-t)图象,图线为开口向下的抛物线,图中所标的量均已知.关于该质点在0-t2时间内的运动,下列说法正确的是( )
如图所示为某质点在0-t2时间内的位移-时间(x-t)图象,图线为开口向下的抛物线,图中所标的量均已知.关于该质点在0-t2时间内的运动,下列说法正确的是( )| A. | 该质点可能做的是曲线运动 | |
| B. | 该质点一定做的是变加速直线运动 | |
| C. | 该质点运动的初速度大小一定是$\frac{2{x}_{0}}{{t}_{1}}$ | |
| D. | 该质点在t=0和t=t2时刻的速度相同 |
2.关于功率公式P=$\frac{W}{t}$t和P=Fv,下列说法正确的有( )
| A. | 据P=$\frac{W}{t}$,知道W和t就可求出任意时刻的功率 | |
| B. | 据P=$\frac{W}{t}$,知道W和t就可求出t内的平均功率 | |
| C. | 从P=Fv知,汽车的功率一定与它的速度成正比 | |
| D. | 从P=Fv知,当功率一定时,牵引力与速度成反比 |
6. 如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下做加速上升运动的一段时间内,以下说法正确的是( )
如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下做加速上升运动的一段时间内,以下说法正确的是( )
 如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下做加速上升运动的一段时间内,以下说法正确的是( )
如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下做加速上升运动的一段时间内,以下说法正确的是( )| A. | 金属棒做得是加速度增加的加速运动 | |
| B. | 力F做的功与安培力做的功的代数和等于棒的机械能增加量 | |
| C. | 金属棒克服安培力做功等于棒产生的电能与回路产生的焦耳热之和 | |
| D. | 力F做的功与重力做的功的代数和等于棒获得的动能和电阻R上放出的热量 |
3.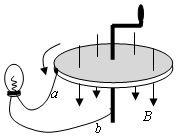 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )| A. | 回路中电流大小恒定 | |
| B. | 回路中电流方向不变,且从b导线流进灯泡,再从a流向旋转的铜盘 | |
| C. | 回路中有大小和方向作周期性变化的电流 | |
| D. | 若将匀强磁场改为仍然垂直穿过铜盘的正弦变化的磁场,不转动铜盘,灯泡中也会有电流流过 |


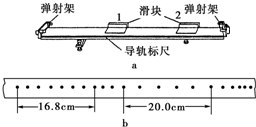 某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.
某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.