题目内容
13. 如图,一水平桌面上固定一半径为R的光滑半圆弧形轨道OQP,圆弧所对的圆心角为180°,在圆弧轨道最左端Q处安装一压力传感器,轨道O处切线与桌面边缘垂直,P处安装一弹簧枪,可发射质量为m的小球.已知重力加速度为g,桌面离水平地面的高度为h,若P处弹簧枪发射一质量为m的小球,运动到Q处时压力传感器的读数为F,则( )
如图,一水平桌面上固定一半径为R的光滑半圆弧形轨道OQP,圆弧所对的圆心角为180°,在圆弧轨道最左端Q处安装一压力传感器,轨道O处切线与桌面边缘垂直,P处安装一弹簧枪,可发射质量为m的小球.已知重力加速度为g,桌面离水平地面的高度为h,若P处弹簧枪发射一质量为m的小球,运动到Q处时压力传感器的读数为F,则( )| A. | 发射的小球的速度为$\sqrt{\frac{FR}{m}}$ | |
| B. | 小球从发射到落地,运动的总时间$π\sqrt{\frac{mR}{F}}$ | |
| C. | 弹簧枪对小球做功为$\frac{FR}{2}$ | |
| D. | 小球落地点到桌子边缘的水平距离为$\sqrt{\frac{2FRh}{mg}}$ |
分析 根据牛顿第二定律,结合Q点压力传感器的示数求出发射小球的速度,根据小球在半圆轨道中的运动时间以及平抛运动的时间求出小球从发射到落地的总时间.根据功能关系求出弹簧枪对小球做功的大小,根据平抛运动的初速度和时间求出水平位移.
解答 解:A、小球在Q点,根据牛顿第二定律有:F=m$\frac{{v}^{2}}{R}$,解得v=$\sqrt{\frac{FR}{m}}$,则发射小球的速度为$\sqrt{\frac{FR}{m}}$,故A正确.
B、小球在半圆形轨道中的运动时间${t}_{1}=\frac{πR}{v}=π\sqrt{\frac{mR}{F}}$,平抛运动的时间${t}_{2}=\sqrt{\frac{2h}{g}}$,则小球从发射到落地,运动的总时间t=$π\sqrt{\frac{mR}{F}}+\sqrt{\frac{2h}{g}}$,故B错误.
C、根据功能关系知,弹簧枪对小球做功W=$\frac{1}{2}m{v}^{2}=\frac{1}{2}FR$,故C正确.
D、小球落地点到桌子边缘的水平距离x=vt=$\sqrt{\frac{FR}{m}}•\sqrt{\frac{2h}{g}}=\sqrt{\frac{2FRh}{mg}}$,故D正确.
故选:ACD.
点评 本题考查了平抛运动和圆周运动的综合运用,知道平抛运动在水平方向和竖直方向上的运动规律以及圆周运动向心力的来源是解决本题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
3.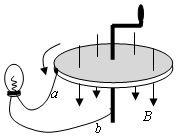 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )| A. | 回路中电流大小恒定 | |
| B. | 回路中电流方向不变,且从b导线流进灯泡,再从a流向旋转的铜盘 | |
| C. | 回路中有大小和方向作周期性变化的电流 | |
| D. | 若将匀强磁场改为仍然垂直穿过铜盘的正弦变化的磁场,不转动铜盘,灯泡中也会有电流流过 |
8.匀加速直线运动的物体的加速度为3m/s2,下列说法正确的是( )
| A. | 任意一秒末的速度总比前一秒初的速度大3m/s | |
| B. | 任意一秒初的速度总比前一秒末的速度大3m/s | |
| C. | 任意一秒的平均速度总比前一秒的平均速度大3m/s | |
| D. | 任意一秒内发生的位移总比前一秒发生的位移大3m |
18. 如图所示,带有负电的摆球,在匀强磁场中摆动,磁场方向垂直纸面向里,摆球通过平衡位置时,相同的物理量是( )
如图所示,带有负电的摆球,在匀强磁场中摆动,磁场方向垂直纸面向里,摆球通过平衡位置时,相同的物理量是( )
 如图所示,带有负电的摆球,在匀强磁场中摆动,磁场方向垂直纸面向里,摆球通过平衡位置时,相同的物理量是( )
如图所示,带有负电的摆球,在匀强磁场中摆动,磁场方向垂直纸面向里,摆球通过平衡位置时,相同的物理量是( )| A. | 悬线对摆球的拉力 | B. | 摆球的动能 | ||
| C. | 摆球的动量 | D. | 摆球所受的合力 |
2.下列有关物理史实的叙述中正确的是( )
| A. | 奥斯特最早提出了电荷周围存在着由它产生的电场 | |
| B. | 密立根发现电子并通过油滴实验精确测定了其电荷量 | |
| C. | 法拉第发现电磁感应现象并得出法拉第电磁感应定律 | |
| D. | 库仑通过库仑扭秤实验得出了两点电荷之间的作用力与其间距的二次方成反比 |
8.关于平抛运动,下列说法正确的是( )
| A. | 平抛运动是加速度和速度都不断增大的曲线运动 | |
| B. | 平抛运动的加速度是恒定的 | |
| C. | 平抛运动的加速度始终与速度方向垂直 | |
| D. | 平抛运动时间足够长时,其速度可以是竖直向下 |
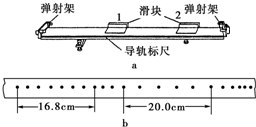 某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.
某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差. 某同学测量一阻值约为20Ω的电阻Rx的阻值,供选择的器材还有:
某同学测量一阻值约为20Ω的电阻Rx的阻值,供选择的器材还有: