题目内容
12.弹簧原长l0=0.15m,受拉力作用后弹簧逐渐伸长,当弹簧伸长到l1=0.2时,作用在弹簧上的力为400N,问:(1)弹簧的劲度系数k为多少?
(2)在该过程中弹力做了多少功?
(3)弹簧的弹性势能变化了多少?
分析 (1)明确形变量,根据胡克定律即可求得劲度系数;
(2)根据功能关系可知,弹力所做的功等于弹性势能的改变量;
(3)根据弹性势能的表达式即可求得弹性势能的改变量.
解答 解:(1)根据F=k(l1-l0)
解得:k=$\frac{F}{{l}_{1}-{l}_{0}}$=$\frac{400}{0.2-0.15}$N/m=8000N/m;
(2)弹力做功等于弹性势能的变化,则W=-$\frac{1}{2}$kx2=-$\frac{1}{2}$×8000×(0.2-0.15)2=-10J;
(3)弹簧的弹性势能增加了△EP=$\frac{1}{2}$kx2=$\frac{1}{2}$×8000×(0.2-0.15)2=10J.
答:(1)弹簧的劲度系数k为8000N/m;
(2)在该过程中弹力做了-10J的功;
(3)弹簧的弹性势能增加了10J.
点评 本题考查功能关系以及弹性势能的表达式,要注意明确弹力做功与弹性势能改变之间的关系,明确弹力做负功时弹性势能增大.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
15. 如图所示为某质点在0-t2时间内的位移-时间(x-t)图象,图线为开口向下的抛物线,图中所标的量均已知.关于该质点在0-t2时间内的运动,下列说法正确的是( )
如图所示为某质点在0-t2时间内的位移-时间(x-t)图象,图线为开口向下的抛物线,图中所标的量均已知.关于该质点在0-t2时间内的运动,下列说法正确的是( )
 如图所示为某质点在0-t2时间内的位移-时间(x-t)图象,图线为开口向下的抛物线,图中所标的量均已知.关于该质点在0-t2时间内的运动,下列说法正确的是( )
如图所示为某质点在0-t2时间内的位移-时间(x-t)图象,图线为开口向下的抛物线,图中所标的量均已知.关于该质点在0-t2时间内的运动,下列说法正确的是( )| A. | 该质点可能做的是曲线运动 | |
| B. | 该质点一定做的是变加速直线运动 | |
| C. | 该质点运动的初速度大小一定是$\frac{2{x}_{0}}{{t}_{1}}$ | |
| D. | 该质点在t=0和t=t2时刻的速度相同 |
3.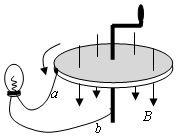 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )| A. | 回路中电流大小恒定 | |
| B. | 回路中电流方向不变,且从b导线流进灯泡,再从a流向旋转的铜盘 | |
| C. | 回路中有大小和方向作周期性变化的电流 | |
| D. | 若将匀强磁场改为仍然垂直穿过铜盘的正弦变化的磁场,不转动铜盘,灯泡中也会有电流流过 |
20.极地卫星的运行轨道平面通过地球的南北两极,轨道可视为圆轨道,若某极地卫星从北极正上方第一次运行至南极正上方,用时间为t,已知地球半径为R,球表面的重力加速度为g,引力常量G,由以上条件可知,( )
| A. | 卫星运行的角速度为$\frac{π}{t}$ | B. | 卫星运行的线速度为π$\frac{R}{t}$ | ||
| C. | 卫星离地面的高度 $\root{3}{\frac{g{R}^{2}{t}^{2}}{{π}^{2}}}$-R | D. | 地球的质量为$\frac{G}{g{R}^{2}}$ |
7.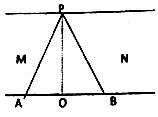 如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )
如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )
 如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )
如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )| A. | TA>TB | B. | TA<TB | ||
| C. | TA=TB | D. | 无法比较TA和TB的大小 |
17.关于机械能守恒,下列说法正确的是( )
| A. | 人乘电梯加速上升的过程,机械能守恒 | |
| B. | 做自由落体运动的物体,机械能一定守恒 | |
| C. | 物休必须在只受重力作用的情况下,机械能才守恒 | |
| D. | 合外力对物体做功为零时,机械能一定守恒 |
2.下列有关物理史实的叙述中正确的是( )
| A. | 奥斯特最早提出了电荷周围存在着由它产生的电场 | |
| B. | 密立根发现电子并通过油滴实验精确测定了其电荷量 | |
| C. | 法拉第发现电磁感应现象并得出法拉第电磁感应定律 | |
| D. | 库仑通过库仑扭秤实验得出了两点电荷之间的作用力与其间距的二次方成反比 |
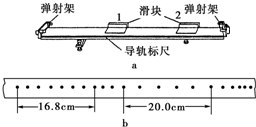 某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.
某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差. 某同学测量一阻值约为20Ω的电阻Rx的阻值,供选择的器材还有:
某同学测量一阻值约为20Ω的电阻Rx的阻值,供选择的器材还有: