题目内容
8.一静止的质量为M的原子核,以相对地的速度v放射出一质量为m的粒子后,原子核剩余部分作反冲运动的速度大小为( )| A. | $\frac{Mv}{m}$ | B. | $\frac{mv}{M-m}$ | C. | $\frac{M-m}{m}$v | D. | $\frac{M+m}{m}$v |
分析 原子核衰变的过程可以认为系统动量守恒.根据动量守恒定律列出等式解决问题.
解答 解:原子核释放粒子的过程系统动量守恒,以释放粒子的速度方向为正方向,由动量守恒定律得:
mv-(M-m)v′=0
解得:v′=$\frac{mv}{M-m}$,故ACD错误,B正确;
故选:B.
点评 本题考查动量守恒定律的应用,注意一般情况下我们运用动量守恒解决问题时要规定正方向,本题中速度中负号表示原子核剩余部分的速度方向与质量为m粒子速度方向相反.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图所示,水平轨道宽为L,轨道区间里存在着斜向上与水平方向夹角为α的匀强磁场.一质量为m的导体棒垂直导轨放置,与导轨右端的距离为s,导体棒与导轨间动摩檫因数为μ.某时刻起给导体棒通以如图所示的恒定电流I,导体棒加速后从轨道右端水平飞出,落在距离水平轨道为h的地面上,落地点与轨道右端的水平距离为s.重力加速度g,忽略空气阻力,则( )
如图所示,水平轨道宽为L,轨道区间里存在着斜向上与水平方向夹角为α的匀强磁场.一质量为m的导体棒垂直导轨放置,与导轨右端的距离为s,导体棒与导轨间动摩檫因数为μ.某时刻起给导体棒通以如图所示的恒定电流I,导体棒加速后从轨道右端水平飞出,落在距离水平轨道为h的地面上,落地点与轨道右端的水平距离为s.重力加速度g,忽略空气阻力,则( )
 如图所示,水平轨道宽为L,轨道区间里存在着斜向上与水平方向夹角为α的匀强磁场.一质量为m的导体棒垂直导轨放置,与导轨右端的距离为s,导体棒与导轨间动摩檫因数为μ.某时刻起给导体棒通以如图所示的恒定电流I,导体棒加速后从轨道右端水平飞出,落在距离水平轨道为h的地面上,落地点与轨道右端的水平距离为s.重力加速度g,忽略空气阻力,则( )
如图所示,水平轨道宽为L,轨道区间里存在着斜向上与水平方向夹角为α的匀强磁场.一质量为m的导体棒垂直导轨放置,与导轨右端的距离为s,导体棒与导轨间动摩檫因数为μ.某时刻起给导体棒通以如图所示的恒定电流I,导体棒加速后从轨道右端水平飞出,落在距离水平轨道为h的地面上,落地点与轨道右端的水平距离为s.重力加速度g,忽略空气阻力,则( )| A. | 导体棒刚飞出轨道时的速度大小为s$\sqrt{\frac{g}{h}}$ | |
| B. | 导体棒在空中飞行的时间为$\sqrt{\frac{2h}{g}}$ | |
| C. | 导体棒在轨道上的加速度大小为$\frac{gs}{4h}$ | |
| D. | 磁感应强度大小为$\frac{mg(s+4μh)}{4hIL(sinα+μcosα)}$ |
19. 如图所示,在竖直平面内有一固定的半圆槽,半圆直径AG水平,B、C、D、E、F点将半圆周六等分.现将5个质量不同的小球1、2、3、4、5(均可视为质点)分别从A点开始向右做平抛运动,分别落到B、C、D、E、F点上,则下列说法正确的是( )
如图所示,在竖直平面内有一固定的半圆槽,半圆直径AG水平,B、C、D、E、F点将半圆周六等分.现将5个质量不同的小球1、2、3、4、5(均可视为质点)分别从A点开始向右做平抛运动,分别落到B、C、D、E、F点上,则下列说法正确的是( )
 如图所示,在竖直平面内有一固定的半圆槽,半圆直径AG水平,B、C、D、E、F点将半圆周六等分.现将5个质量不同的小球1、2、3、4、5(均可视为质点)分别从A点开始向右做平抛运动,分别落到B、C、D、E、F点上,则下列说法正确的是( )
如图所示,在竖直平面内有一固定的半圆槽,半圆直径AG水平,B、C、D、E、F点将半圆周六等分.现将5个质量不同的小球1、2、3、4、5(均可视为质点)分别从A点开始向右做平抛运动,分别落到B、C、D、E、F点上,则下列说法正确的是( )| A. | 球5到达F点时,速度的反方向延长线必过圆心 | |
| B. | 球3做平抛运动全过程速度变化最大 | |
| C. | 球5做平抛运动的时间最长 | |
| D. | 各球到达圆周时球3的重力功率最大 |
16.从高h处以相同的速度先后抛出三个质量相同的球,其中一个上抛一个下抛,另一个平抛,不计空气阻力,则从抛出到落地( )
| A. | 落地时它们的速度相同 | B. | 落地时它们的动能相同 | ||
| C. | 重力的瞬时功率相同 | D. | 重力的平均功率相同 |
3. 如图所示,理想变压器原线圈的a、b两点间输入n=220$\sqrt{2}$sin100πt(V)的电压,副线圈中的R为可变电阻,已知理想变压器原、副线圈的匝数比为10:1,为了使通过原线圈中的电流不超过1A,可变电阻R连入电路的最小阻值是( )
如图所示,理想变压器原线圈的a、b两点间输入n=220$\sqrt{2}$sin100πt(V)的电压,副线圈中的R为可变电阻,已知理想变压器原、副线圈的匝数比为10:1,为了使通过原线圈中的电流不超过1A,可变电阻R连入电路的最小阻值是( )
 如图所示,理想变压器原线圈的a、b两点间输入n=220$\sqrt{2}$sin100πt(V)的电压,副线圈中的R为可变电阻,已知理想变压器原、副线圈的匝数比为10:1,为了使通过原线圈中的电流不超过1A,可变电阻R连入电路的最小阻值是( )
如图所示,理想变压器原线圈的a、b两点间输入n=220$\sqrt{2}$sin100πt(V)的电压,副线圈中的R为可变电阻,已知理想变压器原、副线圈的匝数比为10:1,为了使通过原线圈中的电流不超过1A,可变电阻R连入电路的最小阻值是( )| A. | 2.2Ω | B. | 22$\sqrt{2}$Ω | C. | 220Ω | D. | 220$\sqrt{2}$Ω |
20.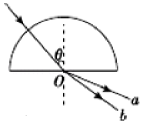 如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
 如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )| A. | 在玻璃中,a光的传播速度小于b光的传播速度 | |
| B. | 在真空中,a光的波长小于b光的波长 | |
| C. | 玻璃砖对a光的折射率小于b光的折射率 | |
| D. | 若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失 | |
| E. | 分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距 |


 如图所示,截面为半圆形的透明圆柱体其折射率为n,圆心为O点,半圆柱体的圆弧部分外表面涂上水银层,可将光线在圆柱面的内表面全部反射.现有一束细光线从直径AB上的M点以入射角θ射入圆柱体的AB界面,经球面反射后恰好在AB界面上的N点发生全反射,设MO长为l1,ON长为l2,求:$\frac{{l}_{1}}{{l}_{2}}$=?
如图所示,截面为半圆形的透明圆柱体其折射率为n,圆心为O点,半圆柱体的圆弧部分外表面涂上水银层,可将光线在圆柱面的内表面全部反射.现有一束细光线从直径AB上的M点以入射角θ射入圆柱体的AB界面,经球面反射后恰好在AB界面上的N点发生全反射,设MO长为l1,ON长为l2,求:$\frac{{l}_{1}}{{l}_{2}}$=?