题目内容
5.如图所示,光滑水平面与一倾斜运输带MP相接,运输带与水平面夹角为θ=30°,运输带顺时针运行,速率v0=5m/s.在水平面上的N点处放一质量m=0.4kg的小物块,N点与运输带下端M点间的距离x=2m.现对小物体施加水平恒力F=10N作用至M点撤掉,连接点M处是平滑的,小物体在此处无碰撞能量损失.小物体与运输带间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,到达运输带最高点P时速度恰好为零,重力加速度g=10m/s2,求: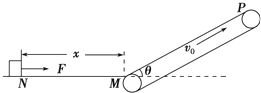
(1)小物体运动到M点时的速度大小;
(2)MP之间的距离L;
(3)小物体在运输带上运动的过程中相对运输带滑动的距离△s.
分析 (1)对物体在水平面上受力分析和做功分析,根据动能定理求小物体运动到M时的速度;
(2)小物体运动到M时的速度大于传送带的速度,物体将在摩擦力作用下做减速运动,根据牛顿第二定律求出加速度和位移,当速度减至与传送带一致时,由于摩擦力小于物体重力沿斜面向下的分力,摩擦力改变方向向上,物体向上做减速运动,速度减为O时到达最高点P,分两段求解物体上滑的位移即可;
(3)根据位移公式求出两段位移以及两段时间内传送带的位移,由几何关系即可求出小物块相对运输带滑动的距离△s.
解答 解:
(1)小物体从N至M点的过程中受重力、支持力和拉力作用,只有拉力对物体做功,根据动能定理有:
$Fx=\frac{1}{2}m{v^2}$
可得:到达M点时小物体的速度$v=\sqrt{\frac{2Fx}{m}}=\sqrt{\frac{2×10×2}{0.4}}m/s=10m/s$
(2)小物体刚到输送带上相对运输带上滑到两者共速前,受沿斜面向下摩擦力,做匀减速运动,令物体的加速度为a1,根据牛顿第二定律有:
mgsinθ+μmgcosθ=ma1
解得a1=$\frac{mgsinθ+μmgcosθ}{m}=gsinθ+μgcosθ$=$10×\frac{1}{2}+\frac{\sqrt{3}}{6}×10×\frac{\sqrt{3}}{2}m/{s}^{2}=7.5m/{s}^{2}$
令此过程中物体上滑的距离为L1,根据速度位移关系有:
$v_0^2-{v^2}=-2{a_1}{L_1}$
解得:L1=$\frac{{v}_{0}^{2}-{v}^{2}}{-2{a}_{1}}=\frac{{5}^{2}-1{0}^{2}}{-2×7.5}m=5m$
小物体与传送带速度相等后,由于μmgcosθ<mgsinθ,所以物体继续做减速运动,相对于传送带下滑,受沿斜面向上摩擦力,令此时物体加速度为a2,则根据牛顿第二定律有:
mgsinθ-μmgcosθ=ma2
加速度a2=$\frac{mgsinθ-μmgcosθ}{m}=gsinθ-μgcosθ=10×\frac{1}{2}-\frac{\sqrt{3}}{6}×10×\frac{\sqrt{3}}{2}$m/s2=2.5m/s2
令物体向上减速至速度为0时的位移为L2,则根据速度位移关系有:
由$0-v_0^2=-2{a_2}{L_2}$
得L2=$\frac{{v}_{0}^{2}}{2{a}_{2}}=\frac{{5}^{2}}{2×2.5}m=5m$
所以MP之间的距离L=L1+L2=5+5m=10m.
(3)令物体速度由v减至v0的时间为t1,则由速度时间关系有:
v0=v-a1t1
得物体第一阶段减速的时间${t}_{1}=\frac{v-{v}_{0}}{{a}_{1}}=\frac{10-5}{7.5}s=\frac{2}{3}s$
所以运输带运行的位移${x_1}={v_0}{t_1}=\frac{10}{3}m$
小物体相对运输带位移$△{s_1}={L_1}-{x_1}=\frac{5}{3}$m
物体由速度v减至0时所用时间为t2,由速度时间关系有:
0=v0-a2t2
得第二阶段减速时间t2=$\frac{{v}_{0}}{{a}_{2}}=\frac{5}{2.5}s=2s$
所以此过程中运输带运行的位移x2=v0t2=10m
小物体相对运输带位移△s2=L2-x2=-5m
小物体相对于运输带的位移:$△s=△{s}_{1}+△{s}_{2}=\frac{5}{3}-5=-\frac{10}{3}$ m
小物体在运输带上运动的过程中相对运输带滑动的距离△s大小为$\frac{10}{3}$m.
答:(1)小物体运动到M时的速度大小为10m/s;
(2)MP之间的距离L=10m;
(3)此过程中小物体与相对运输带滑动的距离△s是$\frac{10}{3}$m
点评 此题考查传送带、受力分析、牛顿第二定律、匀变速直线运动规律、摩擦生热等知识点,熟练掌握相关知识,静下心来分过程研究是解决问题的关键.

| A. | 竖直向上的匀加速运动,加速度a=2m/s2 | |
| B. | 竖直向上的匀减速运动,加速度a=2m/s2 | |
| C. | 竖直向下的匀加速运动,加速度a=2m/s2 | |
| D. | 竖直向下的匀减速运动,加速度a=2m/s2 |
 如图所示,一个质量为m,电荷量为q(q<0)的带电粒子从x轴上的P(a,0)点以速度v,沿与x轴负方向成θ=60°角的方向射入第一象限,并恰好垂直于y轴射出第一象限.在第一象限中存在一有界匀强磁场,磁场的左边界与y轴重合,右边界与直线ON重合,ON与x轴夹角为30°.(不计重力和空气阻力)
如图所示,一个质量为m,电荷量为q(q<0)的带电粒子从x轴上的P(a,0)点以速度v,沿与x轴负方向成θ=60°角的方向射入第一象限,并恰好垂直于y轴射出第一象限.在第一象限中存在一有界匀强磁场,磁场的左边界与y轴重合,右边界与直线ON重合,ON与x轴夹角为30°.(不计重力和空气阻力) 如图所示,在光滑水平面上有一长为L=0.5m的单匝正方形闭合导体线框abcd,处于磁感应强度为B=0.4T的有界匀强磁场中,其ab边与磁场的边界重合.线框由同种粗细均匀、电阻为R=2Ω的导线制成.现用垂直于线框ab边的水平拉力,将线框以速度v=5m/s向右沿水平方向匀速拉出磁场,此过程中保持线框平面与磁感线垂直,且ab边与磁场边界平行.求线框被拉出磁场的过程中:
如图所示,在光滑水平面上有一长为L=0.5m的单匝正方形闭合导体线框abcd,处于磁感应强度为B=0.4T的有界匀强磁场中,其ab边与磁场的边界重合.线框由同种粗细均匀、电阻为R=2Ω的导线制成.现用垂直于线框ab边的水平拉力,将线框以速度v=5m/s向右沿水平方向匀速拉出磁场,此过程中保持线框平面与磁感线垂直,且ab边与磁场边界平行.求线框被拉出磁场的过程中: 如图(a)所示,“
如图(a)所示,“ ”型木块放在光滑水平地面上,木块的水平表面AB粗糙,与水平面夹角θ=37°的表面BC光滑.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.(已知sin37°=0.6,cos37°=0.8,取g=10m/s2.)求:
”型木块放在光滑水平地面上,木块的水平表面AB粗糙,与水平面夹角θ=37°的表面BC光滑.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.(已知sin37°=0.6,cos37°=0.8,取g=10m/s2.)求: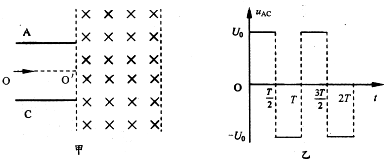
 如图所示,水平地面固定一个足够长的斜面体,倾角θ=37°.一个质量为m=1kg的小滑块受到水平方向的恒力F=10N作用,由静止开始从斜面底端加速上滑,物块运动了s1=34m撤去恒力F,已知小物块与斜面之间的动摩擦因数μ=0.1,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,水平地面固定一个足够长的斜面体,倾角θ=37°.一个质量为m=1kg的小滑块受到水平方向的恒力F=10N作用,由静止开始从斜面底端加速上滑,物块运动了s1=34m撤去恒力F,已知小物块与斜面之间的动摩擦因数μ=0.1,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求: 2012年11月,我国歼-15舰载战斗机首次在“辽宁舰”上成功降落,有关资料表明,该战斗机降落时在水平甲板上受阻拦索的拦阻,滑行s=100m速度从v=80m/s减小到零,若将上述运动视为匀减速直线运动,求:该战斗机在此过程中
2012年11月,我国歼-15舰载战斗机首次在“辽宁舰”上成功降落,有关资料表明,该战斗机降落时在水平甲板上受阻拦索的拦阻,滑行s=100m速度从v=80m/s减小到零,若将上述运动视为匀减速直线运动,求:该战斗机在此过程中