题目内容
16．一个质量为50kg的人，站在升降机的台秤上，当秤的读数为400N时，升降机和人一起做（ ）（g=10m/s2）| A． | 竖直向上的匀加速运动，加速度a=2m/s2 | |
| B． | 竖直向上的匀减速运动，加速度a=2m/s2 | |
| C． | 竖直向下的匀加速运动，加速度a=2m/s2 | |
| D． | 竖直向下的匀减速运动，加速度a=2m/s2 |
分析 由牛顿第二定律可求得升降机的加速度大小及方向，则可判断升降机的运动状态．
解答 解：设向上为正方向；由牛顿第二定律可知：F-mg=ma
解得：a=$\frac{F-mg}{m}=\frac{400-50×10}{50}=-2$m/s2；方向竖直向下；
故物体的运动可能为：加速向下或减速向上运动．故AD错误，BC正确
故选：BC
点评 本题考查超重与失重的知识，在解题时要注意应用牛顿第二定律判断加速度；明确加速度向上有两种可能．
练习册系列答案
相关题目
6．
如图所示，质量不计的弹簧竖直固定在水平面上，t=0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹起离开弹簧，上升到一定高度后再下落，如此反复．通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间t变化的图象如图所示，则（ ）
如图所示，质量不计的弹簧竖直固定在水平面上，t=0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹起离开弹簧，上升到一定高度后再下落，如此反复．通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间t变化的图象如图所示，则（ ）| A． | t1时刻小球速度最大 | |
| B． | t1～t2这段时间内，小球的速度先增大后减小 | |
| C． | t2～t3这段时间内，小球所受合外力一直减小 | |
| D． | t1～t3全过程小球的加速度先减小后增大 |
7．
如图，为一理耦自制变压器，输入端接入交流稳压电源，其电压随时间变化关系e=40$\sqrt{2}$sin 100π（V），负载电阻R=10.0Ω，已知n1、n2的比值为2：1，闭合开关S，则（ ）
如图，为一理耦自制变压器，输入端接入交流稳压电源，其电压随时间变化关系e=40$\sqrt{2}$sin 100π（V），负载电阻R=10.0Ω，已知n1、n2的比值为2：1，闭合开关S，则（ ）| A． | 该交变电流的频率为100Hz | |
| B． | 该负载的电压有效值为20$\sqrt{2}$ V | |
| C． | 负载电荷R所消耗的电功率为40$\sqrt{2}$W | |
| D． | 电路中理想交流电流表A的示数为2.0A |
如图所示，小球（与弹簧不相连）将轻质弹簧压缩后由静止释放，小球在弹力和恒定阻力的作用下沿水平面向右运动．弹簧在弹性限度内，小球从开始运动到与弹簧刚分离的过程中，用v、s、a、F分别表示小球的速度、位移、加速度和所受弹力，t表示时间，规定水平向右为正方向，则下列图象可能正确描述这一运动规律的是（ ）
11．如图甲所示，水平地面上固定一足够长的光滑斜面，斜面顶端有一理想定滑轮，一轻绳跨过滑轮，绳两端分别连接小物块A和B．保持A的质量不变，改变B的质量m，当B的质量连续改变时，得到A的加速度a随B的质量m变化的图线，如图乙所示，设加速度沿斜面向上的方向为正方向，空气阻力不计，重力加速度g取9.8m/s2，斜面的倾角为θ，下列说法正确的是（ ）
| A． | 若θ已知，可求出A的质量 | B． | 若θ未知，可求出乙图中a1的值 | ||
| C． | 若θ已知，可求出乙图中a2的值 | D． | 若θ已知，可求出乙图中m0的值 |
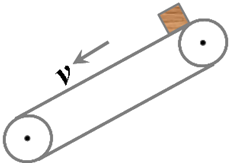如图所示，倾斜传送带与水平方向的夹角为37°，将一小物块轻轻放在正在以速度v=10m/s匀速逆时针传动的传送带的上端，物块和传送带之间的动摩擦因数为?=0.5（设最大静摩擦力等于滑动摩擦力的大小），传送带两皮带轮轴心间的距离为L=16m，求将物块从顶部传到传送带底部所需的时间为多少？（g=10m/s2）若?=0.8，所需的时间为多少？
如图某装卸工要将质量为50Kg的木箱搬到卡车上，找来了长为4.4m的木板，做了一个倾角为37°的斜面．装卸工用大小为550N、方向与斜面平行的斜向上的拉力F将木箱拉上卡车．已知木箱与木板间动摩擦因数μ=0.5，sin37°=0.6，cos37°=0.8，g=10m/s2．
13．
如图所示，ABCD是半径为R的四分之三光滑绝缘圆形轨道，最低点B和最高点D的右侧有竖直向上的匀强电场，场强大小为E．一质量m，带电量+q的小球从A点正上方高h处的F点自由落下，从A点进入圆轨道时无能量损失，不计空气阻力，小球所带电量不变，则（ ）
如图所示，ABCD是半径为R的四分之三光滑绝缘圆形轨道，最低点B和最高点D的右侧有竖直向上的匀强电场，场强大小为E．一质量m，带电量+q的小球从A点正上方高h处的F点自由落下，从A点进入圆轨道时无能量损失，不计空气阻力，小球所带电量不变，则（ ）| A． | 若Eq=4mg，无论h多大，小球总能沿圆轨道到达D点 | |
| B． | 小球从B到D的过程可能作匀速圆周运动 | |
| C． | 调整h和E的大小，可能使小球到达D点时速度为零 | |
| D． | 调整h和E的大小，可能使小球沿圆轨道运动到D点并且水平飞出后到达A点 |