题目内容
18.随着深太空探测的发展,越来越多的“超级类地行星”被发现,某“超级地行星”半径是地球的1.5倍,质量是地球的4倍,下列说法正确是( )| A. | 该星球表面的重力加速度是地球表面的重力加速度的$\frac{9}{16}$倍 | |
| B. | 该星球第一宇宙速度大于地球第一宇宙速度 | |
| C. | 绕该星球运行的卫星的周期是半径相同的绕地球运行卫星周期的$\frac{3}{2}$倍 | |
| D. | 绕该星球运行的卫星的速度是半径相同的绕地球运行卫星速度的$\frac{1}{2}$倍 |
分析 根据万有引力等于重力得出重力加速度的表达式,从而得出星球表面的重力加速度和地球表面重力加速度的关系.根据重力提供向心力求出第一宇宙速度,从而得出星球第一宇宙速度和地球第一宇宙速度的关系.根据万有引力提供向心力求出周期和线速度的表达式,从而分析判断.
解答 解:A、根据$G\frac{Mm}{{R}^{2}}=mg$得星球表面的重力加速度为:g=$\frac{GM}{{R}^{2}}$
因为“超级地行星”半径是地球的1.5倍,质量是地球的4倍,则星球表面的重力加速度是地球表面重力加速度的$\frac{16}{9}$倍,故A错误.
B、根据mg=$m\frac{{v}^{2}}{R}$得星球的第一宇宙速度为:v=$\sqrt{gR}$,因为星球表面的重力加速度是地球表面重力加速度的$\frac{16}{9}$倍,半径是地球的1.5倍,则星球第一宇宙速度是地球第一宇宙速度的$\sqrt{\frac{8}{3}}$倍,即星球第一宇宙速度大于地球第一宇宙速度,故B正确.
CD、根据$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=mr\frac{4{π}^{2}}{{T}^{2}}$得:v=$\sqrt{\frac{GM}{r}}$,T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$,由于质量之比为4:1,半径相等,则绕该星球运行的卫星的周期是半径相同的绕地球运行卫星周期的$\frac{1}{2}$倍,绕该星球运行的卫星的速度是半径相同的绕地球运行卫星速度的2倍,故CD错误.
故选:B.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
9.重为1N的小球,在空中下落了2m的高度后到达地面,下列说法正确的是( )
| A. | 重力对小球做的功一定是2J | B. | 小球的重力势能一定增加了2J | ||
| C. | 小球刚下落时的重力势能一定是2J | D. | 落地时小球的重力势能一定是0 |
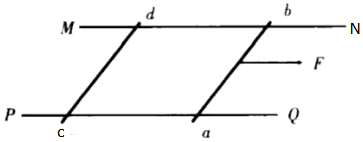
6. 自行车和人的总质量为 m,在一水平地面运动,人可以视为质点.若自行车以速度 v 转过半径为 R 的 弯道,车所在平面的倾角为 θ,如图所示.下列说法中正确的是( )
自行车和人的总质量为 m,在一水平地面运动,人可以视为质点.若自行车以速度 v 转过半径为 R 的 弯道,车所在平面的倾角为 θ,如图所示.下列说法中正确的是( )
 自行车和人的总质量为 m,在一水平地面运动,人可以视为质点.若自行车以速度 v 转过半径为 R 的 弯道,车所在平面的倾角为 θ,如图所示.下列说法中正确的是( )
自行车和人的总质量为 m,在一水平地面运动,人可以视为质点.若自行车以速度 v 转过半径为 R 的 弯道,车所在平面的倾角为 θ,如图所示.下列说法中正确的是( )| A. | 自行车受到的支持力为$\frac{mg}{sinθ}$ | B. | 自行车所受地面的摩擦为0N | ||
| C. | 自行车所受地面的摩擦为m$\frac{{v}^{2}}{R}$ | D. | 自行车的倾角满足关系:tan=$\frac{gR}{{v}^{2}}$ |
13. 如图甲所示,“滑滑梯”是小朋友喜爱的游戏活动.小朋友在室内“滑滑梯”的运动可简化为小物体从静止出发,先沿斜板下滑,再进入水平地面的过程,如图乙所示.某次游戏中,一位小朋友(可视为质点)从斜板顶端静止出发后到达房间右侧墙面时刚好停止.已知斜板倾角为θ,斜板顶端在水平地面的投影点到房间右侧墙面的距离为斜板长度的2倍,小朋友与斜板及水平地面间的动摩擦因数均为μ,不计小朋友从斜板进入水平地面时的能量损失,则θ与μ应满足的关系是( )
如图甲所示,“滑滑梯”是小朋友喜爱的游戏活动.小朋友在室内“滑滑梯”的运动可简化为小物体从静止出发,先沿斜板下滑,再进入水平地面的过程,如图乙所示.某次游戏中,一位小朋友(可视为质点)从斜板顶端静止出发后到达房间右侧墙面时刚好停止.已知斜板倾角为θ,斜板顶端在水平地面的投影点到房间右侧墙面的距离为斜板长度的2倍,小朋友与斜板及水平地面间的动摩擦因数均为μ,不计小朋友从斜板进入水平地面时的能量损失,则θ与μ应满足的关系是( )
 如图甲所示,“滑滑梯”是小朋友喜爱的游戏活动.小朋友在室内“滑滑梯”的运动可简化为小物体从静止出发,先沿斜板下滑,再进入水平地面的过程,如图乙所示.某次游戏中,一位小朋友(可视为质点)从斜板顶端静止出发后到达房间右侧墙面时刚好停止.已知斜板倾角为θ,斜板顶端在水平地面的投影点到房间右侧墙面的距离为斜板长度的2倍,小朋友与斜板及水平地面间的动摩擦因数均为μ,不计小朋友从斜板进入水平地面时的能量损失,则θ与μ应满足的关系是( )
如图甲所示,“滑滑梯”是小朋友喜爱的游戏活动.小朋友在室内“滑滑梯”的运动可简化为小物体从静止出发,先沿斜板下滑,再进入水平地面的过程,如图乙所示.某次游戏中,一位小朋友(可视为质点)从斜板顶端静止出发后到达房间右侧墙面时刚好停止.已知斜板倾角为θ,斜板顶端在水平地面的投影点到房间右侧墙面的距离为斜板长度的2倍,小朋友与斜板及水平地面间的动摩擦因数均为μ,不计小朋友从斜板进入水平地面时的能量损失,则θ与μ应满足的关系是( )| A. | sinθ=μ | B. | sinθ=2μ | C. | sinθ=3μ | D. | sinθ=4μ |
3.美国医生用I123对老布什总统进行诊疗,使其很快恢复健康,关于I123的特性正确的是( )
| A. | 半衰期长,并能迅速从体内清除 | B. | 半衰期长,并能缓慢从体内清除 | ||
| C. | 半衰期短,并能迅速从体内清除 | D. | 半衰期短,并能缓慢从体内清除 |
 如图所示,绷紧的传送带始终保持着大小υ=6m/s的速度匀速运动.一质量m=1kg的小物块无初速地放在皮带的左端A处,A与B之间距离S=9m,小物块到达B端时速度恰好与传送带速度相等,取g=10m/s2,求物块从A运动到B的过程中,
如图所示,绷紧的传送带始终保持着大小υ=6m/s的速度匀速运动.一质量m=1kg的小物块无初速地放在皮带的左端A处,A与B之间距离S=9m,小物块到达B端时速度恰好与传送带速度相等,取g=10m/s2,求物块从A运动到B的过程中, 如图所示木板的质量为9m长为L,静止在光滑的水平地面上.木板的左端放有一个质量为0.9m的木块(可视为质点),一颗质量为0.1m的子弹以v0的水平初速度打入木块并留在木块中,最后木块刚好没有离开木板,子弹与木块作用时间极短.求:
如图所示木板的质量为9m长为L,静止在光滑的水平地面上.木板的左端放有一个质量为0.9m的木块(可视为质点),一颗质量为0.1m的子弹以v0的水平初速度打入木块并留在木块中,最后木块刚好没有离开木板,子弹与木块作用时间极短.求: 如图是检验某种防护罩承受冲击能力的装置模型,M为固定于竖直平面内半径为R=0.9m的光滑半圆弧轨道,A、B分别是轨道的最低点和最高点.N为防护罩,它是一个竖直固定的$\frac{1}{4}$圆弧,圆心位于B点,半径r=$\frac{{\sqrt{10}}}{5}$m,在A处水平放置一个弹簧枪,可向M轨道发射速度大小不同的小钢珠,弹簧枪可将弹性势能完全转化为小钢珠的动能.某次实验中,弹簧枪发射一个质量m=0.02kg的小钢珠,沿轨道运动恰好能经过B点,水平飞出后落到N的某一点上(图中未画出),取g=10m/s2.求本次实验:
如图是检验某种防护罩承受冲击能力的装置模型,M为固定于竖直平面内半径为R=0.9m的光滑半圆弧轨道,A、B分别是轨道的最低点和最高点.N为防护罩,它是一个竖直固定的$\frac{1}{4}$圆弧,圆心位于B点,半径r=$\frac{{\sqrt{10}}}{5}$m,在A处水平放置一个弹簧枪,可向M轨道发射速度大小不同的小钢珠,弹簧枪可将弹性势能完全转化为小钢珠的动能.某次实验中,弹簧枪发射一个质量m=0.02kg的小钢珠,沿轨道运动恰好能经过B点,水平飞出后落到N的某一点上(图中未画出),取g=10m/s2.求本次实验: