题目内容
13. 如图甲所示,“滑滑梯”是小朋友喜爱的游戏活动.小朋友在室内“滑滑梯”的运动可简化为小物体从静止出发,先沿斜板下滑,再进入水平地面的过程,如图乙所示.某次游戏中,一位小朋友(可视为质点)从斜板顶端静止出发后到达房间右侧墙面时刚好停止.已知斜板倾角为θ,斜板顶端在水平地面的投影点到房间右侧墙面的距离为斜板长度的2倍,小朋友与斜板及水平地面间的动摩擦因数均为μ,不计小朋友从斜板进入水平地面时的能量损失,则θ与μ应满足的关系是( )
如图甲所示,“滑滑梯”是小朋友喜爱的游戏活动.小朋友在室内“滑滑梯”的运动可简化为小物体从静止出发,先沿斜板下滑,再进入水平地面的过程,如图乙所示.某次游戏中,一位小朋友(可视为质点)从斜板顶端静止出发后到达房间右侧墙面时刚好停止.已知斜板倾角为θ,斜板顶端在水平地面的投影点到房间右侧墙面的距离为斜板长度的2倍,小朋友与斜板及水平地面间的动摩擦因数均为μ,不计小朋友从斜板进入水平地面时的能量损失,则θ与μ应满足的关系是( )| A. | sinθ=μ | B. | sinθ=2μ | C. | sinθ=3μ | D. | sinθ=4μ |
分析 小朋友在斜板上做加速运动,在水平面做减速运动,整个过程只有重力与摩擦力做功,应用动能定理可以求出θ与μ间的关系.
解答 解:设斜板的长度为L,对整个过程,由动能定理得:
mgLsinθ-μmgcosθ•L-μmg(2L-Lcosθ)=0-0,
解得:sinθ=2μ.
故选:B
点评 本题考查了动能定理的应用,分析清楚小朋友的运动过程是解题的前提,应用动能定理可以解题,本题也可以对两个过程分别应用动能定理解题.

练习册系列答案
相关题目
4.下列说法正确的是( )
| A. | 热量可以由低温物体传递到高温物体 | |
| B. | 外界对物体做功,物体的内能必定增加 | |
| C. | 若容器中用活塞封闭着刚饱和的一些水汽,当保持温度不变缓慢移动活塞使容器的体积减小时,水汽的质量减少,密度增大 | |
| D. | 不可能从单一热源吸收热量并把它全部用来做功,而不引起其他变化 | |
| E. | 在“用油膜法估测分子的大小”的实验中,将油酸酒精溶液的体积直接作为油酸的体积进行计算,会使分子直径计算结果偏大 |
1. 如图所示,一轻绳通过无摩擦的小定滑轮O与小球B连接,另一端与套在光滑竖直杆上的小物块A连接,杆两端固定且足够长.物块A由静止从图示位置释放后,先沿杆向上运动.设某时刻物块A运动的速度大小为vA,小球B运动的速度大小为vB,轻绳与杆的夹角为θ(θ<90°),则( )
如图所示,一轻绳通过无摩擦的小定滑轮O与小球B连接,另一端与套在光滑竖直杆上的小物块A连接,杆两端固定且足够长.物块A由静止从图示位置释放后,先沿杆向上运动.设某时刻物块A运动的速度大小为vA,小球B运动的速度大小为vB,轻绳与杆的夹角为θ(θ<90°),则( )
 如图所示,一轻绳通过无摩擦的小定滑轮O与小球B连接,另一端与套在光滑竖直杆上的小物块A连接,杆两端固定且足够长.物块A由静止从图示位置释放后,先沿杆向上运动.设某时刻物块A运动的速度大小为vA,小球B运动的速度大小为vB,轻绳与杆的夹角为θ(θ<90°),则( )
如图所示,一轻绳通过无摩擦的小定滑轮O与小球B连接,另一端与套在光滑竖直杆上的小物块A连接,杆两端固定且足够长.物块A由静止从图示位置释放后,先沿杆向上运动.设某时刻物块A运动的速度大小为vA,小球B运动的速度大小为vB,轻绳与杆的夹角为θ(θ<90°),则( )| A. | vB=vAcosθ | |
| B. | vA=vBcosθ | |
| C. | 小球B向下运动过程中,其动能一直增大 | |
| D. | 物块A上升到与滑轮等高处时,它的机械能最大 |
8. 如图是一种升降电梯的示意图,A为载人箱,B为平衡重物,它们的质量均为M,上下均有跨过滑轮的钢索系住,在电动机的牵引下使电梯上下运动.如果电梯中载人的总质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h高度后停止.不计空气和摩擦阻力的情况,重力加速度为g,则( )
如图是一种升降电梯的示意图,A为载人箱,B为平衡重物,它们的质量均为M,上下均有跨过滑轮的钢索系住,在电动机的牵引下使电梯上下运动.如果电梯中载人的总质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h高度后停止.不计空气和摩擦阻力的情况,重力加速度为g,则( )
 如图是一种升降电梯的示意图,A为载人箱,B为平衡重物,它们的质量均为M,上下均有跨过滑轮的钢索系住,在电动机的牵引下使电梯上下运动.如果电梯中载人的总质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h高度后停止.不计空气和摩擦阻力的情况,重力加速度为g,则( )
如图是一种升降电梯的示意图,A为载人箱,B为平衡重物,它们的质量均为M,上下均有跨过滑轮的钢索系住,在电动机的牵引下使电梯上下运动.如果电梯中载人的总质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h高度后停止.不计空气和摩擦阻力的情况,重力加速度为g,则( )| A. | 上升高度为$\frac{{(2M+m)v}^{2}}{2mg}$ | B. | 上升高度为$\frac{{(m+M)v}^{2}}{2mg}$ | ||
| C. | 此过程中钢索的拉力为$\frac{2M(m+M)g}{2M+m}$ | D. | 此过程中钢索的拉力为$\frac{2m(m+M)g}{2M+m}$ |
18.随着深太空探测的发展,越来越多的“超级类地行星”被发现,某“超级地行星”半径是地球的1.5倍,质量是地球的4倍,下列说法正确是( )
| A. | 该星球表面的重力加速度是地球表面的重力加速度的$\frac{9}{16}$倍 | |
| B. | 该星球第一宇宙速度大于地球第一宇宙速度 | |
| C. | 绕该星球运行的卫星的周期是半径相同的绕地球运行卫星周期的$\frac{3}{2}$倍 | |
| D. | 绕该星球运行的卫星的速度是半径相同的绕地球运行卫星速度的$\frac{1}{2}$倍 |
5. 如图所示,一半径为R的光滑半圆形细轨道,其圆心为O,竖直固定在地面上.轨道正上方离地高为h处固定一水平光滑长直细杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方.A、B是质量均为m的小环,A套在杆上,B套在轨道上,一条不可伸长的轻绳通过定滑轮连接两环.两环均可看做质点,且不计滑轮大小与摩擦.现对A环施加一水平向右的力F,使B环从地面由静止开始沿轨道运动.则下列说法正确的是( )
如图所示,一半径为R的光滑半圆形细轨道,其圆心为O,竖直固定在地面上.轨道正上方离地高为h处固定一水平光滑长直细杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方.A、B是质量均为m的小环,A套在杆上,B套在轨道上,一条不可伸长的轻绳通过定滑轮连接两环.两环均可看做质点,且不计滑轮大小与摩擦.现对A环施加一水平向右的力F,使B环从地面由静止开始沿轨道运动.则下列说法正确的是( )
 如图所示,一半径为R的光滑半圆形细轨道,其圆心为O,竖直固定在地面上.轨道正上方离地高为h处固定一水平光滑长直细杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方.A、B是质量均为m的小环,A套在杆上,B套在轨道上,一条不可伸长的轻绳通过定滑轮连接两环.两环均可看做质点,且不计滑轮大小与摩擦.现对A环施加一水平向右的力F,使B环从地面由静止开始沿轨道运动.则下列说法正确的是( )
如图所示,一半径为R的光滑半圆形细轨道,其圆心为O,竖直固定在地面上.轨道正上方离地高为h处固定一水平光滑长直细杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方.A、B是质量均为m的小环,A套在杆上,B套在轨道上,一条不可伸长的轻绳通过定滑轮连接两环.两环均可看做质点,且不计滑轮大小与摩擦.现对A环施加一水平向右的力F,使B环从地面由静止开始沿轨道运动.则下列说法正确的是( )| A. | 若缓慢拉动A环,B环缓慢上升至D点的过程中,F一直减小 | |
| B. | 若缓慢拉动A环,B环缓慢上升至D点的过程中,外力F所做的功小于B环机械能的增加量 | |
| C. | 若F为恒力,B环最终将静止在D点 | |
| D. | 若F为恒力,B环被拉到与A环速度大小相等时,有sin∠OPB=$\frac{R}{h}$ |
2. 原子核的平均结合能与原子序数有如图所示的关系.下列关于原子核结构和核反应的说法中正确的是( )
原子核的平均结合能与原子序数有如图所示的关系.下列关于原子核结构和核反应的说法中正确的是( )
 原子核的平均结合能与原子序数有如图所示的关系.下列关于原子核结构和核反应的说法中正确的是( )
原子核的平均结合能与原子序数有如图所示的关系.下列关于原子核结构和核反应的说法中正确的是( )| A. | 原子核a和b聚变成原子核c时会有质量亏损,要放出能量 | |
| B. | 原子核f裂变成原子核d和e时会有质量增加,要吸收能量 | |
| C. | 原子核c中核子的平均质量要比原子核b的大 | |
| D. | 原子核f中核子的平均质量要比原子核e的小 |
2. 摆长为L的单摆在匀强磁场中摆动,摆动中摆线始终紧绷,若摆球带正电,电荷量为q,质量为m,磁感应强度为B,开始时悬系偏离竖直方向θ角,当摆球从最高点第一次摆到最低点时,摆线对小球的拉力大小为( )
摆长为L的单摆在匀强磁场中摆动,摆动中摆线始终紧绷,若摆球带正电,电荷量为q,质量为m,磁感应强度为B,开始时悬系偏离竖直方向θ角,当摆球从最高点第一次摆到最低点时,摆线对小球的拉力大小为( )
 摆长为L的单摆在匀强磁场中摆动,摆动中摆线始终紧绷,若摆球带正电,电荷量为q,质量为m,磁感应强度为B,开始时悬系偏离竖直方向θ角,当摆球从最高点第一次摆到最低点时,摆线对小球的拉力大小为( )
摆长为L的单摆在匀强磁场中摆动,摆动中摆线始终紧绷,若摆球带正电,电荷量为q,质量为m,磁感应强度为B,开始时悬系偏离竖直方向θ角,当摆球从最高点第一次摆到最低点时,摆线对小球的拉力大小为( )| A. | mg(3-2cosθ)-qB$\sqrt{2gL(1-cosθ)}$ | B. | mg(3+2cosθ)-qB$\sqrt{2gL(1-cosθ)}$ | ||
| C. | mg(3-2cosθ)+qB$\sqrt{2gL(1-cosθ)}$ | D. | mg(3+2cosθ)+qB$\sqrt{2gL(1-cosθ)}$ |
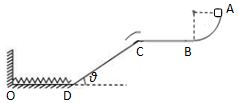 如图,质量为m=1kg的小滑块(视为质点)在半径为R=0.4m的$\frac{1}{4}$圆弧A端由静止开始释放,它运动到B点时速度为v=2m/s.当滑块经过B后立即将圆弧轨道撤去.滑块在光滑水平面上运动一段距离后,通过换向轨道由C点过渡到倾角为θ=37°、长s=1m的斜面CD上,CD之间铺了一层匀质特殊材料,其与滑块间的动摩擦系数可在0≤μ≤1.5之间调节.斜面底部D点与光滑地面平滑相连,地面上一根轻弹簧一端固定在O点,自然状态下另一端恰好在D点.认为滑块通过C和D前后速度大小不变,最大静摩擦力等于滑动摩擦力.取g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.
如图,质量为m=1kg的小滑块(视为质点)在半径为R=0.4m的$\frac{1}{4}$圆弧A端由静止开始释放,它运动到B点时速度为v=2m/s.当滑块经过B后立即将圆弧轨道撤去.滑块在光滑水平面上运动一段距离后,通过换向轨道由C点过渡到倾角为θ=37°、长s=1m的斜面CD上,CD之间铺了一层匀质特殊材料,其与滑块间的动摩擦系数可在0≤μ≤1.5之间调节.斜面底部D点与光滑地面平滑相连,地面上一根轻弹簧一端固定在O点,自然状态下另一端恰好在D点.认为滑块通过C和D前后速度大小不变,最大静摩擦力等于滑动摩擦力.取g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.