题目内容
8. 如图所示,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以$\frac{{v}_{0}}{2}$的速率弹回,而B球以$\frac{v_0}{3}$的速率向右运动,求A、B两球的质量之比为2:9.
如图所示,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以$\frac{{v}_{0}}{2}$的速率弹回,而B球以$\frac{v_0}{3}$的速率向右运动,求A、B两球的质量之比为2:9.
分析 以A、B两球组成的系统为研究对象,在碰撞过程中,系统动量守恒,由动量守恒定律可以求出两球的质量之比.
解答 解:以A、B组成的系统为研究对象,以A球的初速度方向为正方向,由动量守恒定律得:
mAv0=mA(-$\frac{{v}_{0}}{2}$)+mB($\frac{v_0}{3}$)
解得:$\frac{{m}_{A}}{{m}_{B}}$=$\frac{2}{9}$
即A、B两球的质量之比为2:9.
故答案为:2:9
点评 两球碰撞过程中遵守基本规律:动量守恒定律,由动量守恒定律求两球质量之比是常见的题型,要熟练掌握,解题时要注意选取正方向.

练习册系列答案
相关题目
18.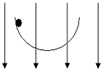 一个绝缘光滑半圆环轨道放在竖直向下的匀强电场中,场强为E,在环的上端,一个质量为m,带电量为+q的小球由静止开始沿轨道运动,则( )
一个绝缘光滑半圆环轨道放在竖直向下的匀强电场中,场强为E,在环的上端,一个质量为m,带电量为+q的小球由静止开始沿轨道运动,则( )
 一个绝缘光滑半圆环轨道放在竖直向下的匀强电场中,场强为E,在环的上端,一个质量为m,带电量为+q的小球由静止开始沿轨道运动,则( )
一个绝缘光滑半圆环轨道放在竖直向下的匀强电场中,场强为E,在环的上端,一个质量为m,带电量为+q的小球由静止开始沿轨道运动,则( )| A. | 小球运动过程中机械能守恒 | B. | 小球运动的过程中机械能减少 | ||
| C. | 在最低点球对轨道的压力为(mg+Eq) | D. | 在最低点球对轨道的压力为3(mg+Eq) |
19. 卫星1和卫星2在同一轨道上绕地球做匀速圆周运动,圆心为O,轨道半径为r,某时刻两颗卫星分别位于轨道上的A、B两位置,两卫星与地心O连线间的夹角为60°,如图所示,若卫星均沿顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力,下列判断正确的是( )
卫星1和卫星2在同一轨道上绕地球做匀速圆周运动,圆心为O,轨道半径为r,某时刻两颗卫星分别位于轨道上的A、B两位置,两卫星与地心O连线间的夹角为60°,如图所示,若卫星均沿顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力,下列判断正确的是( )
 卫星1和卫星2在同一轨道上绕地球做匀速圆周运动,圆心为O,轨道半径为r,某时刻两颗卫星分别位于轨道上的A、B两位置,两卫星与地心O连线间的夹角为60°,如图所示,若卫星均沿顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力,下列判断正确的是( )
卫星1和卫星2在同一轨道上绕地球做匀速圆周运动,圆心为O,轨道半径为r,某时刻两颗卫星分别位于轨道上的A、B两位置,两卫星与地心O连线间的夹角为60°,如图所示,若卫星均沿顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力,下列判断正确的是( )| A. | 这两颗卫星的加速度大小均为$\frac{{{R^2}g}}{r^2}$ | |
| B. | 卫星1由A第一次运动到B所用的时间为$\frac{πr}{3R}\sqrt{\frac{r}{g}}$ | |
| C. | 卫星1向后喷气就一定能原二者共同的轨道追上卫星2 | |
| D. | 卫星1追击卫星2的过程中,两者的万有引力大小均不变 |
3.关于功率,下列说法中正确的是( )
| A. | 功率是用来描述物体做功多少的物理量 | |
| B. | 功率大,做的功一定多 | |
| C. | 功率小,做的功一定少 | |
| D. | 做功越快,功率越大 |
13.一质点做简谐运动,振幅是4cm、频率是2.5Hz,该质点从平衡位置起向正方向运动,经2.9s质点的位移和路程分别是(选初始运动方向为正方向)( )
| A. | 4 cm,24 cm | B. | 4 cm,116 cm | C. | 零,100 cm | D. | -4 cm,116 cm |
20. 如图所示,一球体绕轴O1O2以角速度ω旋转,A、B为球体上两点,下列几种说法中正确的是( )
如图所示,一球体绕轴O1O2以角速度ω旋转,A、B为球体上两点,下列几种说法中正确的是( )
 如图所示,一球体绕轴O1O2以角速度ω旋转,A、B为球体上两点,下列几种说法中正确的是( )
如图所示,一球体绕轴O1O2以角速度ω旋转,A、B为球体上两点,下列几种说法中正确的是( )| A. | A、B两点具有相同的角速度 | |
| B. | A、B两点具有相同的线速度 | |
| C. | A、B两点的向心加速度方向都指向球心 | |
| D. | A、B两点的向心加速度相同 |
17.平抛物体的初速度为10m/s,当水平方向分位移与竖直方向分位移相等时( )
| A. | 水平分速度与竖直分速度大小相等 | B. | 瞬时速率vt=20m/s | ||
| C. | 位移大小等于20m | D. | 运动的时间t=2s |
 水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道向右运动,如图所示,小球进入圆形轨道后刚好能通过c点,然后小球做平抛运动落在直轨道上的d点,则:
水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道向右运动,如图所示,小球进入圆形轨道后刚好能通过c点,然后小球做平抛运动落在直轨道上的d点,则: 如图所示为粮仓的传送带装置,一倾斜固定的传送带与水平方向成α=30°,且以恒定的大小为v0=2m/s的速度匀速向上传动,工人将一质量为m=50kg的粮袋由底端无初速地放到传送带上,经一段时间,粮袋运动到距离地面为h=2m的高处,粮袋与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{2}$,g=10m/s2
如图所示为粮仓的传送带装置,一倾斜固定的传送带与水平方向成α=30°,且以恒定的大小为v0=2m/s的速度匀速向上传动,工人将一质量为m=50kg的粮袋由底端无初速地放到传送带上,经一段时间,粮袋运动到距离地面为h=2m的高处,粮袋与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{2}$,g=10m/s2