题目内容
16. 水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道向右运动,如图所示,小球进入圆形轨道后刚好能通过c点,然后小球做平抛运动落在直轨道上的d点,则:
水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道向右运动,如图所示,小球进入圆形轨道后刚好能通过c点,然后小球做平抛运动落在直轨道上的d点,则:(1)小球到达c点的速度大小?
(2)小球从c点落到d点所需时间?
(3)小球在直轨道上的落点d与b点水平距离为多少?
(4)小球落地时速度大小?
分析 (1)根据牛顿第二定律,抓住C点弹力为零,靠重力提供向心力,求出小球到达c点的速度.
(2)根据高度,结合位移司机公式求出平抛运动的时间.
(3)根据初速度和时间求出平抛运动的水平位移.
(4)根据速度时间公式求出落地时的竖直分速度,结合平行四边形定则求出落地的速度.
解答 解:(1)小球在c点时,由牛顿第二定律得:
mg=$m\frac{{{v}_{c}}^{2}}{R}$,解得vc=$\sqrt{gR}$,
(2)小球在c点做平抛运动,由运动学公式得:
2R=$\frac{1}{2}$gt2.解得t=$\sqrt{\frac{4R}{g}}$,
(3)平抛运动在水平方向上做匀速直线运动,则x=${v}_{c}t=\sqrt{gR}\sqrt{\frac{4R}{g}}$=2R.
(4)小球落地时竖直分速度${v}_{y}=gt=g\sqrt{\frac{4R}{g}}=\sqrt{4gR}$,
根据平行四边形定则知,在d点落地速度$v=\sqrt{{{v}_{c}}^{2}+{{v}_{y}}^{2}}=\sqrt{gR+4gR}$=$\sqrt{5gR}$.
答:(1)小球到达c点的速度大小为$\sqrt{gR}$;
(2)小球从c点落到d点所需时间为$\sqrt{\frac{4R}{g}}$;
(3)小球在直轨道上的落点d与b点水平距离为2R;
(4)小球落地时速度大小为$\sqrt{5gR}$.
点评 本题考查了平抛运动和圆周运动的综合运用,知道平抛运动在水平方向和竖直方向上的运动规律,以及圆周运动向心力的来源是解决本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
6.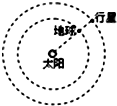 某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
 某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )| A. | ($\frac{N}{N-1}$)${\;}^{\frac{2}{3}}$ | B. | ($\frac{N+1}{N}$)${\;}^{\frac{3}{2}}$ | C. | ($\frac{N}{N-1}$)${\;}^{\frac{3}{2}}$ | D. | ($\frac{N+1}{N}$)${\;}^{\frac{2}{3}}$ |
7.静止在地球上的物体都要随地球一起转动,下列说法正确的是( )
| A. | 它们的线速度大小相同 | B. | 它们的角速度大小相同 | ||
| C. | 它们的向心加速度大小相同 | D. | 它们的向心加速度方向不变 |
11.下列说法中正确的是( )
| A. | 物体的速度越大,加速度一定越大 | |
| B. | 物体的速度变化得越快,加速度越大 | |
| C. | 物体的加速度不断减小,速度一定越来越小 | |
| D. | 物体在某时刻的速度为零,其加速度也一定为零 |
1.关于匀速圆周运动,下列说法中正确的是( )
| A. | 线速度的大小和方向都不变 | |
| B. | 向心加速度的大小和方向都不变 | |
| C. | 周期和角速度都不变 | |
| D. | 向心力的方向总是沿轨迹的切线方向 |
5.关于交流电的有效值和最大值,下列说法正确的是( )
| A. | 任何形式的交流电压的有效值是U=$\frac{{U}_{m}}{\sqrt{2}}$的关系 | |
| B. | 只有正弦交流电才具有U=$\frac{{U}_{m}}{\sqrt{2}}$的关系 | |
| C. | 照明电压220V,动力电压380V指的都是有效值 | |
| D. | 交流电压表和电流表测量的是交流电的最大值 |
6.如图一个面积为S的矩形线圈在匀强磁场中做匀速转动下列说法正确的是( )

| A. | t1时刻线圈平面位于中性面位置 | B. | t2时刻ad的速度方向跟磁感线平行 | ||
| C. | t3时刻线圈平面与中性面重合 | D. | 在甲图位置电流方向改变一次 |
 在“研究平抛物体的运动”实验中
在“研究平抛物体的运动”实验中 如图所示,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以$\frac{{v}_{0}}{2}$的速率弹回,而B球以$\frac{v_0}{3}$的速率向右运动,求A、B两球的质量之比为2:9.
如图所示,小球A以速率v0向右运动时跟静止的小球B发生碰撞,碰后A球以$\frac{{v}_{0}}{2}$的速率弹回,而B球以$\frac{v_0}{3}$的速率向右运动,求A、B两球的质量之比为2:9.