题目内容
4. 如图所示,在倾角为θ的斜面顶端O点,以不同的水平速度抛出一小球.当以初速度v1抛出时,小球经过时间t1落到斜面的中点a;当以初速度v2抛出时,小球经过时间t2落到斜面的底端b,则 ( )
如图所示,在倾角为θ的斜面顶端O点,以不同的水平速度抛出一小球.当以初速度v1抛出时,小球经过时间t1落到斜面的中点a;当以初速度v2抛出时,小球经过时间t2落到斜面的底端b,则 ( )| A. | ${t_2}=\sqrt{2}{t_1}$ | B. | t2=2t1 | C. | v2=$\sqrt{2}$v1 | D. | v2=2v1 |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据竖直位移之比求出平抛运动的时间关系,从而结合水平位移求出初速度的关系.
解答 解:AB、小球落在A点和B点,下降的高度之比为1:2,根据$h=\frac{1}{2}g{t}_{\;}^{2}$知,t=$\sqrt{\frac{2h}{g}}$,则小球落在A点和B点的时间之比为1:$\sqrt{2}$,即${t}_{2}^{\;}=\sqrt{2}{t}_{1}^{\;}$,故A正确,B错误;
CD、因为水平位移之比为1:2,则初速度之比为:$1:\sqrt{2}$,即${v}_{2}^{\;}=\sqrt{2}{v}_{1}^{\;}$.故D错误,C正确.
故选:AC
点评 本题就是对平抛运动规律的考查,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
15. 如图所示,长为L的细绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳与竖直方向的夹角为θ.下列说法中正确的是( )
如图所示,长为L的细绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳与竖直方向的夹角为θ.下列说法中正确的是( )
 如图所示,长为L的细绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳与竖直方向的夹角为θ.下列说法中正确的是( )
如图所示,长为L的细绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳与竖直方向的夹角为θ.下列说法中正确的是( )| A. | 小球受重力、细绳的拉力和向心力作用 | |
| B. | θ 越大,小球运动的线速度越大 | |
| C. | θ 越大,小球运动的周期越大 | |
| D. | θ 越大,小球运动的向心加速度越小 |
19. 如图所示,木板AB与水平地面间的夹角为θ,一物块被一与木板始终垂直的外力F压在木板上.在缓慢抬起木板B端使θ角增大(始终小于90°)的过程中,外力F的大小保持不变,物块始终相对木板静止.下列说法正确的是( )
如图所示,木板AB与水平地面间的夹角为θ,一物块被一与木板始终垂直的外力F压在木板上.在缓慢抬起木板B端使θ角增大(始终小于90°)的过程中,外力F的大小保持不变,物块始终相对木板静止.下列说法正确的是( )
 如图所示,木板AB与水平地面间的夹角为θ,一物块被一与木板始终垂直的外力F压在木板上.在缓慢抬起木板B端使θ角增大(始终小于90°)的过程中,外力F的大小保持不变,物块始终相对木板静止.下列说法正确的是( )
如图所示,木板AB与水平地面间的夹角为θ,一物块被一与木板始终垂直的外力F压在木板上.在缓慢抬起木板B端使θ角增大(始终小于90°)的过程中,外力F的大小保持不变,物块始终相对木板静止.下列说法正确的是( )| A. | 物块所受的合力逐渐增大 | B. | 物块对木板的弹力逐渐减小 | ||
| C. | 物块所受摩擦力逐渐增大 | D. | 物块所受的摩擦力先减小后增大 |
9. 如图甲所示,用传送带运送相同的物体,水平传送带沿顺时针方向匀速运转.每次都从传送带左端P由静止轻轻放上一个物体,物体经时间t=10s到达传送带右端Q.若每次释放物体时作为t=0时刻,正常运送过程中物体的速度图象如图乙所示.若某次运送过程中,中途出现了传送带突然停止运动的情况,结果被传送的物体恰好到达了传送带的右端Q.由以上条件可知(重力加速度g=10/s2)( )
如图甲所示,用传送带运送相同的物体,水平传送带沿顺时针方向匀速运转.每次都从传送带左端P由静止轻轻放上一个物体,物体经时间t=10s到达传送带右端Q.若每次释放物体时作为t=0时刻,正常运送过程中物体的速度图象如图乙所示.若某次运送过程中,中途出现了传送带突然停止运动的情况,结果被传送的物体恰好到达了传送带的右端Q.由以上条件可知(重力加速度g=10/s2)( )
 如图甲所示,用传送带运送相同的物体,水平传送带沿顺时针方向匀速运转.每次都从传送带左端P由静止轻轻放上一个物体,物体经时间t=10s到达传送带右端Q.若每次释放物体时作为t=0时刻,正常运送过程中物体的速度图象如图乙所示.若某次运送过程中,中途出现了传送带突然停止运动的情况,结果被传送的物体恰好到达了传送带的右端Q.由以上条件可知(重力加速度g=10/s2)( )
如图甲所示,用传送带运送相同的物体,水平传送带沿顺时针方向匀速运转.每次都从传送带左端P由静止轻轻放上一个物体,物体经时间t=10s到达传送带右端Q.若每次释放物体时作为t=0时刻,正常运送过程中物体的速度图象如图乙所示.若某次运送过程中,中途出现了传送带突然停止运动的情况,结果被传送的物体恰好到达了传送带的右端Q.由以上条件可知(重力加速度g=10/s2)( )| A. | 传送带的长度为36m | |
| B. | 物体与传送带间的动摩擦因数为0.2 | |
| C. | 传送带停止的时刻为t=9s的时刻 | |
| D. | 传送带停止后物体运动的平均速度大小为4m/s |
 如图所示,在方向水平向右的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点,当小球静止在B点时,细线与竖直方向夹角θ=30°问:
如图所示,在方向水平向右的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点,当小球静止在B点时,细线与竖直方向夹角θ=30°问:
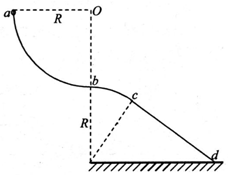 如图所示,竖直面内两段半径均为R的圆形轨道和一段直轨道相连在一起.其中ab部分为$\frac{1}{4}$圆弧,bc部务为弧长为$\frac{πR}{6}$的一段圆弧,两段圆弧在b点的切线为同一条水平线;直线轨道cd的c点与圆弧相切,d点固定在水平地面上.一表面光滑质量为m的小圆环套在轨道上并从a点由静止释放后,圆环可沿轨道自由下滑.已知b点与地面相距R,重力加速度大小为g,求:
如图所示,竖直面内两段半径均为R的圆形轨道和一段直轨道相连在一起.其中ab部分为$\frac{1}{4}$圆弧,bc部务为弧长为$\frac{πR}{6}$的一段圆弧,两段圆弧在b点的切线为同一条水平线;直线轨道cd的c点与圆弧相切,d点固定在水平地面上.一表面光滑质量为m的小圆环套在轨道上并从a点由静止释放后,圆环可沿轨道自由下滑.已知b点与地面相距R,重力加速度大小为g,求:
