题目内容
16.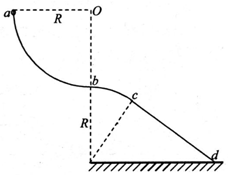 如图所示,竖直面内两段半径均为R的圆形轨道和一段直轨道相连在一起.其中ab部分为$\frac{1}{4}$圆弧,bc部务为弧长为$\frac{πR}{6}$的一段圆弧,两段圆弧在b点的切线为同一条水平线;直线轨道cd的c点与圆弧相切,d点固定在水平地面上.一表面光滑质量为m的小圆环套在轨道上并从a点由静止释放后,圆环可沿轨道自由下滑.已知b点与地面相距R,重力加速度大小为g,求:
如图所示,竖直面内两段半径均为R的圆形轨道和一段直轨道相连在一起.其中ab部分为$\frac{1}{4}$圆弧,bc部务为弧长为$\frac{πR}{6}$的一段圆弧,两段圆弧在b点的切线为同一条水平线;直线轨道cd的c点与圆弧相切,d点固定在水平地面上.一表面光滑质量为m的小圆环套在轨道上并从a点由静止释放后,圆环可沿轨道自由下滑.已知b点与地面相距R,重力加速度大小为g,求:(1)圆环通过ab圆弧的最低点b时所受轨道的支持力大小;
(2)圆环在直轨道cd上运动的时间.
分析 (1)小圆环由a到b过程中机械能守恒,再对最低点由牛顿第二定律和向心力公式可求得支持力大小;
(2)根据可求得夹角大小以及cd间的距离,再对ac过程由机械能守恒定律和平均速度公式,联立即可求得在cd上的时间.
解答 解:(1)小圆环由a到b机械能守恒
则有:mgR=$\frac{1}{2}$mvb2
在最低端b点时由牛顿第二定律得:
F-mg=m$\frac{{v}_{b}^{2}}{R}$
解得:F=3mg;
(2)由题意知:θ=$\frac{S}{R}$=$\frac{π}{6}$
xcd=$\frac{R}{tanθ}$=$\sqrt{3}$R;
小圆环由a到c机械能守恒
mgR(2-cosθ)=$\frac{1}{2}$mvd2
小圆环由c到d的平均速度
v=$\frac{{v}_{C}+{v}_{d}}{2}$
小圆环由c到d运动的时间
t=$\frac{{x}_{cd}}{v}$=(4-2$\sqrt{4-\sqrt{3}}$)$\frac{\sqrt{Rg}}{8}$
答:(1)圆环通过ab圆弧的最低点b时所受轨道的支持力大小为mg;
(2)圆环在直轨道cd上运动的时间(4-2$\sqrt{4-\sqrt{3}}$)$\frac{\sqrt{Rg}}{8}$
点评 本题考查机械能守恒定律的应用以及运动学规律的应用,要注意正确分析物理过程,做好受力分析,才能准确选择合适的物理规律求解.

练习册系列答案
相关题目
7.如图所示,A、B分别是甲、乙两小球从同一地点沿同一直线运动的v-t图象,根据图象可以判断( )

| A. | 在t=5s时,两球相距最远 | |
| B. | 在t=6s时,甲球的速率小于乙球的速率 | |
| C. | 在t=6s时,甲球的加速度小于乙球的加速度 | |
| D. | 在t=8s时,两球相遇 |
4. 如图所示,在倾角为θ的斜面顶端O点,以不同的水平速度抛出一小球.当以初速度v1抛出时,小球经过时间t1落到斜面的中点a;当以初速度v2抛出时,小球经过时间t2落到斜面的底端b,则 ( )
如图所示,在倾角为θ的斜面顶端O点,以不同的水平速度抛出一小球.当以初速度v1抛出时,小球经过时间t1落到斜面的中点a;当以初速度v2抛出时,小球经过时间t2落到斜面的底端b,则 ( )
 如图所示,在倾角为θ的斜面顶端O点,以不同的水平速度抛出一小球.当以初速度v1抛出时,小球经过时间t1落到斜面的中点a;当以初速度v2抛出时,小球经过时间t2落到斜面的底端b,则 ( )
如图所示,在倾角为θ的斜面顶端O点,以不同的水平速度抛出一小球.当以初速度v1抛出时,小球经过时间t1落到斜面的中点a;当以初速度v2抛出时,小球经过时间t2落到斜面的底端b,则 ( )| A. | ${t_2}=\sqrt{2}{t_1}$ | B. | t2=2t1 | C. | v2=$\sqrt{2}$v1 | D. | v2=2v1 |
1. a、b两物体的质量分别为m1,m2,由轻质弹簧相连.当用恒力F竖直向上拉着a,使a、b一起向上做匀加速直线运动时,弹簧伸长量为x1,当用大小仍为F的恒力沿水平方向拉着a,使a、b一起沿光滑水平桌面做匀加速直线运动时,弹簧伸长量为x2( )
a、b两物体的质量分别为m1,m2,由轻质弹簧相连.当用恒力F竖直向上拉着a,使a、b一起向上做匀加速直线运动时,弹簧伸长量为x1,当用大小仍为F的恒力沿水平方向拉着a,使a、b一起沿光滑水平桌面做匀加速直线运动时,弹簧伸长量为x2( )
 a、b两物体的质量分别为m1,m2,由轻质弹簧相连.当用恒力F竖直向上拉着a,使a、b一起向上做匀加速直线运动时,弹簧伸长量为x1,当用大小仍为F的恒力沿水平方向拉着a,使a、b一起沿光滑水平桌面做匀加速直线运动时,弹簧伸长量为x2( )
a、b两物体的质量分别为m1,m2,由轻质弹簧相连.当用恒力F竖直向上拉着a,使a、b一起向上做匀加速直线运动时,弹簧伸长量为x1,当用大小仍为F的恒力沿水平方向拉着a,使a、b一起沿光滑水平桌面做匀加速直线运动时,弹簧伸长量为x2( )| A. | x1一定等于x2 | B. | 若m1>m2,则x1<x2 | C. | x1一定大于x2 | D. | 若m1>m2,则x1>x2 |
5.某物体的运动经仪器监控扫描,输入计算机后得到物体的位移x(m)和时间t(s)的关系式为:x=6t-t2.则物体( )
| A. | 初速度为6m/s | B. | 加速度为1m/s2 | ||
| C. | 前4 s的位移是8 m | D. | 前4 s的路程是8 m |




 在验证力的平行四边形定则的实验中,使用的装置如图所示.其中弹簧秤a的轴线与橡皮条垂直,则a、b两弹簧秤中b(选填“a”或“b”)的示数较大;若使弹簧秤b由图示位置开始沿顺时针方向缓慢转过一个角度,在这个过程中,保持O点位置不变和弹簧秤a的拉伸方向不变,则整个过程中弹簧秤a的示数变大,弹簧秤b的示数变大. (选填“变大”、“变小”或“不变”)
在验证力的平行四边形定则的实验中,使用的装置如图所示.其中弹簧秤a的轴线与橡皮条垂直,则a、b两弹簧秤中b(选填“a”或“b”)的示数较大;若使弹簧秤b由图示位置开始沿顺时针方向缓慢转过一个角度,在这个过程中,保持O点位置不变和弹簧秤a的拉伸方向不变,则整个过程中弹簧秤a的示数变大,弹簧秤b的示数变大. (选填“变大”、“变小”或“不变”) 如图所示,水平面上的小车内固定一个倾角为30°的光滑斜面,平行于斜面的细绳一端固定在车顶上,另一端系着一个质量为m的物体,不计空气阻力,重力加速度为g;
如图所示,水平面上的小车内固定一个倾角为30°的光滑斜面,平行于斜面的细绳一端固定在车顶上,另一端系着一个质量为m的物体,不计空气阻力,重力加速度为g;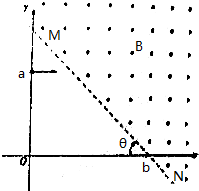 如图所示,纸面内有一直角坐标系xOy,a、b为坐标轴上的两点,其坐标分别为(0,2l)、(3l,0),直线MN过b点且可根据需要绕b点在纸面内转动,MN右侧存在垂直纸面向外的匀强磁场,磁感应强度大小为B,一质量为m,电荷量为q(q>0)的带电粒子从a点平行x轴射入第一象限,若MN绕b点转到合适位置,就能保证粒子经过磁场偏转后恰好能够到达b点,设MN与x轴负方向的夹角为θ,不计粒子重力.
如图所示,纸面内有一直角坐标系xOy,a、b为坐标轴上的两点,其坐标分别为(0,2l)、(3l,0),直线MN过b点且可根据需要绕b点在纸面内转动,MN右侧存在垂直纸面向外的匀强磁场,磁感应强度大小为B,一质量为m,电荷量为q(q>0)的带电粒子从a点平行x轴射入第一象限,若MN绕b点转到合适位置,就能保证粒子经过磁场偏转后恰好能够到达b点,设MN与x轴负方向的夹角为θ,不计粒子重力.