��Ŀ����
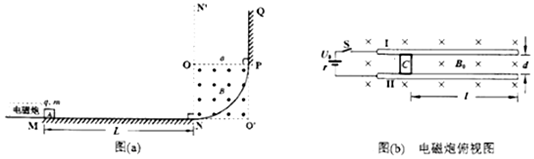
9����ͼ��a����ʾ����Ե���MNPQλ��ͬһ��ֱ���ڣ�����MN��ˮƽ��PQ����ֱ��NP��Ϊ�⻬��$\frac{1}{4}$Բ����Բ��ΪO���뾶Ϊa����������M�㴦����һ����Ϊm�������Ϊq��q��0�������A��ֱ��NN���Ҳ��з���ˮƽ���ҵĵ糡��ͼ��δ����������ǿΪE=$\frac{mg}{q}$���ڰ���Բ�����NP��ONO��P�����з���ֱֽ���������ǿ�ų����ڹ��M�������һ����ˮƽ�⻬�����ϵĿɷ���ġ��ڵ����ĵ����ģ�ͣ���ṹͼ��ͼ��b����ʾ��������������ȳ���ƽ�й⻬����I��II���Դ�Ϳ���S��������Դ�ĵ綯��ΪU0������Ϊr������I��II���Ϊd��������Բ��ƣ����ڵ�����һ����Ϊ2m������ΪR�IJ����絼���C��C�պ���I��II���ܽӴ��������������Ҷ�Ϊl��C�ĵ�������MN��ͬһˮƽ���ϣ���������ڴ��ھ��ȴų��У��ų�������ֱ���£��Ÿ�Ӧǿ�ȴ�СΪB0���������ٶ�Ϊg��������C�ڵ������˶�ʱ�ĵ�Ÿ�Ӧ����A��C����Ϊ�ʵ㣬����A���˶��������������һֱδ�䣮��1����C��A��ײǰ���ٶ�v0�Ĵ�С��
��2����A��C����ײΪ������ײ��A��C��MN����Ļ���Ħ��������ͬ��������Aǡ�ܵ���P�㣬��C����ֹͣλ�õ�M��ľ��룻
��3��������Aǡ�ܵ���P�㣬��Ҫ��A�˶�ʱʼ�ղ��뿪Բ���������ONO��P�����ڴų��ĴŸ�Ӧǿ��BӦ�����������
���� ��1���ȸ���ŷķ�������ͨ�����ڵ����Ļ�·�ĵ��������ɶ��ܶ�����C��A��ײǰ���ٶ�v0�Ĵ�С��
��2��A��C����ײΪ������ײ�����ݶ����غ�Ͷ����غ���ʽ���õ��������ߵ��ٶȱ���ʽ��A��NN���Ҳ��ܵ��ĵ糡����������С��ȣ������͵糡���ĺ�����СΪ$\sqrt{2}$mg������ֱ��OQб�����£�N��P����Գƣ�ҪAǡ�ܵ���P��ֻ��A�յ���N�㼴�ɣ��ɶ��ܶ�����⣮
��3����A��P����N��ʱ����������ָ��O�㣬A�����뿪������ɶ��ܶ����������غ㶨�ɣ������ѧ֪ʶ��⣮
��� �⣺��1��ͨ�����ڵ����Ļ�·�ĵ���Ϊ I=$\frac{E}{R+r}$
��C���ɶ��ܶ�����
F��L=$\frac{1}{2}•2m{v}_{0}^{2}$
�� F��=B0Id
������� v0=$\sqrt{\frac{{B}_{0}Edl}{��R+r��m}}$��
��2��A��C����ȫ������ײ��ȡ����Ϊ�������ɶ����غ㶨�ɺͶ����غ�ã�
2mv0=mvA+2mvC��
$\frac{1}{2}•$2mv02=$\frac{1}{2}•$mvA2+$\frac{1}{2}•$2mvC2��
������ã�vA=$\frac{4}{3}{v}_{0}$=$\frac{4}{3}$$\sqrt{\frac{{B}_{0}Edl}{��R+r��m}}$��vC=$\frac{1}{3}{v}_{0}$=$\frac{1}{3}$$\sqrt{\frac{{B}_{0}Edl}{��R+r��m}}$��
A��NN���Ҳ��ܵ��ĵ糡�� F=qE=q$\frac{mg}{q}$=mg
�����͵糡���ĺ�����СΪ F��=$\sqrt{2}$mg������ֱ��OQб�����£�N��P����Գƣ�ҪAǡ�ܵ���P��ֻ��A�յ���N�㼴�ɣ���Ħ������Ϊ�̣�C��ֹʱ��M��ľ���Ϊlx����
��mgL=$\frac{1}{2}m{v}_{A}^{2}$
��•mglx=$\frac{1}{2}•2m{v}_{C}^{2}$
������� lx=$\frac{L}{16}$��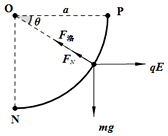
��3����A��P����N��ʱ����������ָ��O�㣬A�����뿪�������A���OPת���Ƚ�ʱ�����ٶ�Ϊv���Թ����ѹ��ΪFN����
FN+qvB-mgsin��-qEcos��=m$\frac{{v}^{2}}{a}$
�������غ�� mgasin��-qEa��1-cos�ȣ�=$\frac{1}{2}m{v}^{2}$
Ҫʹ��A���뿪�������� FN��0��������� B��$\frac{m\sqrt{g}��3sin��+3cos��-2��}{q\sqrt{2a}\sqrt{��sin��+cos��-1��}}$
��Ϊ f���ȣ�=$\frac{3sin��+3cos��-2}{\sqrt{sin��+cos��-1}}$=3$\sqrt{sin��+cos��-1}$+$\frac{1}{\sqrt{sin��+cos��-1}}$
��3$\sqrt{sin��+cos��-1}$=$\frac{1}{\sqrt{sin��+cos��-1}}$ʱ����sin��+cos��=$\frac{4}{3}$ʱ��f���ȣ�=f���ȣ�min=2$\sqrt{3}$
��B��$\frac{m\sqrt{g}}{q\sqrt{2a}}$��2$\sqrt{3}$=$\frac{m}{q}$$\sqrt{\frac{6g}{a}}$=Bmax��
���ǵ���ֵ��Ҫ��sin��+cos��=$\frac{4}{3}$�����οɵ� 1��sin����+$\frac{��}{4}$��=$\frac{\frac{4}{3}}{\sqrt{2}}$��$\frac{1}{\sqrt{2}}$=sin$\frac{��}{4}$����֪����[0����/4]��Χ���н⣬˵�����������Ǻ����ģ���B��ȡֵӦ����������ǣ�
B��Bmax=$\frac{m}{q}$$\sqrt{\frac{6g}{a}}$��
��
��1��C��A��ײǰ���ٶ�v0�Ĵ�СΪ$\sqrt{\frac{{B}_{0}Edl}{��R+r��m}}$��
��2����A��C����ײΪ������ײ��A��C��MN����Ļ���Ħ��������ͬ��������Aǡ�ܵ���P�㣬C����ֹͣλ�õ�M��ľ�����$\frac{L}{16}$��
��3��������Aǡ�ܵ���P�㣬��Ҫ��A�˶�ʱʼ�ղ��뿪Բ�������ONO��P�����ڴų��ĴŸ�Ӧǿ��BӦ�����������B��$\frac{m}{q}$$\sqrt{\frac{6g}{a}}$��
���� �������Ĺؼ���Ҫ������������˶����̣�������ѧ֪ʶ��ֵ���ֶ�Ӧ�ö��ܶ�����ţ�ٵڶ����ɺ������غ㶨�ɽ����о���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | �������ܼ�С��1900 J | B�� | �������ܼ�С��2000 J | ||
| C�� | ����������1900 J | D�� | ����������2000 J |
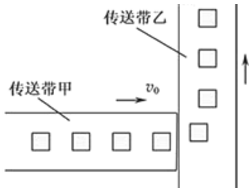 ��ͼ��ʾ�������������������ֱ�ҵȸߵ�ˮƽ���ʹ����ң����ٶ�Ϊv0��С�����뿪��ǰ����ٶ���ͬ����ƽ�ȵش������ϣ���������֮��Ķ�Ħ������Ϊ�̣��ҵĿ����㹻���������ٶ�Ϊg��������
��ͼ��ʾ�������������������ֱ�ҵȸߵ�ˮƽ���ʹ����ң����ٶ�Ϊv0��С�����뿪��ǰ����ٶ���ͬ����ƽ�ȵش������ϣ���������֮��Ķ�Ħ������Ϊ�̣��ҵĿ����㹻���������ٶ�Ϊg��������| A�� | ���ҵ��ٶ�Ϊ v0�����������ϲ��� ��ֱ���ҵ��˶��������ľ���s=$\frac{{{v}_{0}}^{2}}{2g��}$ | |
| B�� | ���ҵ��ٶ�Ϊ 2v0�������ӻ����ҵ������ϲ���ֹͣ���õ�ʱ�䲻�� | |
| C�� | ���ҵ��ٶ�Ϊ 2v0�����������ϸ�ֹͣ����ʱ���ٶȴ�Сv=2v0 | |
| D�� | �����ҵ��ٶ� 2v0 ���䣬�����������ϸ�ֹͣ����ʱ����һֻ����ǡ�ô������ϣ���˷�������ÿ��������������Ϊm���������봫�ʹ�֮��Ħ���⣬����������ľ����ƣ������ҵĵ綯����ƽ���������$\overline{P}$=$\frac{4\sqrt{5}}{5}$mg��v0 |
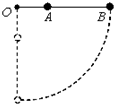 ��ͼ��ʾ����Ϊ3l������ϸ��һ�˿���O������ת�������Ͼ�O��l��3l���ֱ�̶�������Ϊm��С��A��B���ֽ�ϸ������ˮƽ�����ɾ�ֹ�ͷţ�����һ��Ħ������������������ˮƽת����ֱλ�ù����У�������
��ͼ��ʾ����Ϊ3l������ϸ��һ�˿���O������ת�������Ͼ�O��l��3l���ֱ�̶�������Ϊm��С��A��B���ֽ�ϸ������ˮƽ�����ɾ�ֹ�ͷţ�����һ��Ħ������������������ˮƽת����ֱλ�ù����У�������| A�� | �˹���A���е���غ㣬B���е���غ� | |
| B�� | �˹���A���е�ܼ��٣�B���е������ | |
| C�� | ���˵�����ֱλ��ʱ����B���ٶȴ�СΪ2$\sqrt{\frac{gl}{5}}$ | |
| D�� | ���˴ﵽ��ֱλ��ʱ��OA�θ˶����������СΪ$\frac{26}{5}$mg |
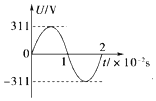
| A�� | �ý������Ƶ��Ϊ100Hz | |
| B�� | �ý��������ЧֵΪ311V | |
| C�� | �ý������������2s | |
| D�� | �ý������˲ʱֵ����ʽΪu=311sin100��t��V�� |
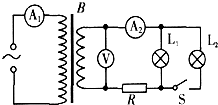 ͼ��BΪ�����ѹ�������ڽ����ѹ��Чֵ���ֲ���ĵ�Դ�ϣ�ָʾ��L1��L2��ȫ��ͬ������ֵ���㶨���䣩��R��һ����ֵ���裬��ѹ������������Ϊ����������ʼʱ����S�DZպϵģ���S�Ͽ�������˵����ȷ���ǣ�������
ͼ��BΪ�����ѹ�������ڽ����ѹ��Чֵ���ֲ���ĵ�Դ�ϣ�ָʾ��L1��L2��ȫ��ͬ������ֵ���㶨���䣩��R��һ����ֵ���裬��ѹ������������Ϊ����������ʼʱ����S�DZպϵģ���S�Ͽ�������˵����ȷ���ǣ�������| A�� | ������A2��ʾ����� | B�� | ������A1��ʾ����С | ||
| C�� | ��ѹ����ʾ����� | D�� | ����L1�����ȱ䰵 |
 ��ͼ��ʾ������MN�Ҳ����һ����ֱ���ϵ���ǿ�ų���һ�߳�ΪL�������ε��Ѿ��Ƚ����߿�abcd���ڹ⻬ˮƽ���ϣ�����ΪR������Ϊm��ab���ڴų�������MN���߽߱磮t=0ʱ��Ÿ�Ӧǿ��B��ʱ��t�ı仯������B=��t����Ϊ������ij�������ͬʱ��һˮƽ����ʹ��Ȧ���ھ�ֹ״̬�������������Բ��ƣ�
��ͼ��ʾ������MN�Ҳ����һ����ֱ���ϵ���ǿ�ų���һ�߳�ΪL�������ε��Ѿ��Ƚ����߿�abcd���ڹ⻬ˮƽ���ϣ�����ΪR������Ϊm��ab���ڴų�������MN���߽߱磮t=0ʱ��Ÿ�Ӧǿ��B��ʱ��t�ı仯������B=��t����Ϊ������ij�������ͬʱ��һˮƽ����ʹ��Ȧ���ھ�ֹ״̬�������������Բ��ƣ�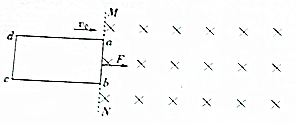 ��ͼ��ʾ���ھ�Եˮƽ�����Ϸ���һ���ν����߿�abcd������MN�Ҳ�ֲ���һ��ֱ���µ���ǿ�ų�����֪�ų��ĴŸ�Ӧǿ��B=0.5T���߿�߳�lab=0.2m��lcb=0.5m������m=0.1kg������R=0.1�����߿�������Ķ�Ħ��������=0.2������һˮƽ���ҵ�����F�������߿��ϣ�ʹ����v0=1m/s���ٶ����������˶�һ�ξ��룬�������ٶ�gȡ10m2/s����
��ͼ��ʾ���ھ�Եˮƽ�����Ϸ���һ���ν����߿�abcd������MN�Ҳ�ֲ���һ��ֱ���µ���ǿ�ų�����֪�ų��ĴŸ�Ӧǿ��B=0.5T���߿�߳�lab=0.2m��lcb=0.5m������m=0.1kg������R=0.1�����߿�������Ķ�Ħ��������=0.2������һˮƽ���ҵ�����F�������߿��ϣ�ʹ����v0=1m/s���ٶ����������˶�һ�ξ��룬�������ٶ�gȡ10m2/s����