题目内容
9.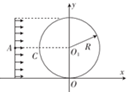 如图所示,x轴正方向水平向右,y轴正方向竖直向上,在xOy平面内存在与y轴平行的匀强电场,圆心在O1(0,R)、半径为R的圆形区域内存在与xOy平面垂直的匀强磁场,在O1的左边垂直x轴放置一微粒发射装置,它可在0<y<2R的范围内沿x轴正方向发射出大量质量均为m、电荷量均为q、初速度均为v的带负电微粒.重力加速度为g.
如图所示,x轴正方向水平向右,y轴正方向竖直向上,在xOy平面内存在与y轴平行的匀强电场,圆心在O1(0,R)、半径为R的圆形区域内存在与xOy平面垂直的匀强磁场,在O1的左边垂直x轴放置一微粒发射装置,它可在0<y<2R的范围内沿x轴正方向发射出大量质量均为m、电荷量均为q、初速度均为v的带负电微粒.重力加速度为g.(1)若从微粒发射装置上的A点(AO1水平)射出的带电微粒平行于x轴从C点进入磁场区域,并从坐标原点O沿y轴负方向离开,求电场的电场强度和磁场的磁感应强度的大小和方向;
(2)若其他条件不变,只将磁场反向,求从发射装置上距x轴$\frac{R}{2}$处射出的微粒离开圆形磁场区域时的位置坐标以及该微粒在磁场中运动的时间;
(3)若其他条件不变,只将这些带电微粒的初速度变为2v,请分析并判断它们与x轴相交的区域范围.
分析 (1)根据粒子进入磁场前做直线运动,得到竖直方向受力平衡,进而得到电场强度;再根据粒子在磁场中的偏转得到偏转圆半径及磁场方向,然后由洛伦兹力做向心力得到磁感应强度大小;
(2)磁场反向,偏转方向反向,根据几何关系求得出射点即中心角,然后根据周期公式求得运动时间;
(3)分析不同位置粒子的运动情况,得到交点与偏转角度的关系,偏转角度与发射位置的关系,进而得到交点范围.
解答 解:(1)从微粒发射装置上的A点(AO1水平)射出的带电微粒平行于x轴从C点进入磁场区域,那么粒子在A到C过程中只受重力、电场力作用,且在竖直方向上合外力为零,即重力和电场力平衡,所以,电场方向沿y轴负方向,电场强度$E=\frac{mg}{q}$;
带电微粒平行于x轴从C点进入磁场区域,并从坐标原点O沿y轴负方向离开,所以,根据偏转方向,由左手定则可得磁感应强度方向:垂直xOy平面向里;
且粒子做圆周运动的半径为R,所以,由洛伦兹力做向心力,即$Bvq=\frac{m{v}^{2}}{R}$可得:$B=\frac{mv}{qR}$;
(2)若其他条件不变,只将磁场反向,则粒子在磁场中运动半径不变,偏转方向相反,所以,粒子运动轨迹如图所示,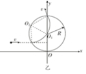 ,
,
所以,由偏转圆半径、磁场区域半径都为R,且粒子进入磁场时的速度水平向右,对应半径竖直向上,可得粒子从磁场区域最高点即(0,2R)离开磁场,
粒子在磁场中转过的中心角为$90°+arcsin\frac{R-\frac{1}{2}R}{R}=120°$,所以,粒子在磁场中的运动时间$t=\frac{1}{3}T=\frac{2πR}{3v}$;
(3)当微粒的初速度变为2v,由洛伦兹力做向心力可知,粒子运动半径r=2R;
粒子在磁场中经过一段圆弧运动后离开磁场做匀速直线运动,在最上方的粒子趋向与一直做匀速直线运动;发射位置下移,粒子经偏转后打在x轴上,且越向下,偏转角度越大,粒子打在x轴上越近;在最下方的粒子直接打在O点,故粒子与x轴相交的区域范围为x>0;
答:(1)若从微粒发射装置上的A点(AO1水平)射出的带电微粒平行于x轴从C点进入磁场区域,并从坐标原点O沿y轴负方向离开,那么电场的电场强度大小为$\frac{mg}{q}$,方向沿y轴负方向;磁场的磁感应强度的大小为$\frac{mv}{qR}$,方向:垂直xOy平面向里;
(2)若其他条件不变,只将磁场反向,那么从发射装置上距x轴$\frac{R}{2}$处射出的微粒离开圆形磁场区域时的位置坐标为(0,2R),该微粒在磁场中运动的时间为$\frac{2πR}{3v}$;
(3)若其他条件不变,只将这些带电微粒的初速度变为2v,则它们与x轴相交的区域范围为x>0.
点评 带电粒子的运动问题,先对粒子进行受力分析求得加速度,然后根据几何关系即加速度求得运动状态.

 名校课堂系列答案
名校课堂系列答案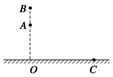 如图所示,在水平地面上O点正上方不同高度的A、B两点分别水平抛出一小球,如果两球均落在同一点C上,则两小球( )
如图所示,在水平地面上O点正上方不同高度的A、B两点分别水平抛出一小球,如果两球均落在同一点C上,则两小球( )| A. | 落地的速度大小可能相等 | B. | 落地的速度方向可能相同 | ||
| C. | 落地的时间可能相等 | D. | 抛出时的速度可能相同 |
 来自太阳和其他星体的宇宙射线中含有大量高能带电粒子,若这些粒子都直接到达地面,将会对地球上的生命带来危害;但由于地磁场(如图所示)的存在改变了宇宙射线中带电粒子的运动方向,使得很多高能带电粒子不能到达地面.若不考虑地磁偏角的影响,关于上述高能带电粒子在地磁场的作用下运动情况的判断,下列说法中正确的是:( )
来自太阳和其他星体的宇宙射线中含有大量高能带电粒子,若这些粒子都直接到达地面,将会对地球上的生命带来危害;但由于地磁场(如图所示)的存在改变了宇宙射线中带电粒子的运动方向,使得很多高能带电粒子不能到达地面.若不考虑地磁偏角的影响,关于上述高能带电粒子在地磁场的作用下运动情况的判断,下列说法中正确的是:( )| A. | 若带电粒子带正电,且沿地球赤道平面射向地心,则由于地磁场的作用将向东偏转 | |
| B. | 若带电粒子带正电,且沿地球赤道平面射向地心,则由于地磁场的作用将向西偏转 | |
| C. | 对于在南极上空水平匀速飞行的飞机,飞行员左侧边机翼末端的电势高于右侧机翼末端的电势 | |
| D. | 若带电粒子沿垂直地球赤道平面射向地心,它可能在地磁场中做匀速圆周运动 |
 如图所示,两个异种点电荷-Q1,+Q2固定在一条直线上,虚线是以-Q1,+Q2所在点为圆心的两个圆,a,b是两个圆的交点,c,d是两个圆与直线的交点.下列说法正确的是( )
如图所示,两个异种点电荷-Q1,+Q2固定在一条直线上,虚线是以-Q1,+Q2所在点为圆心的两个圆,a,b是两个圆的交点,c,d是两个圆与直线的交点.下列说法正确的是( )| A. | 把一质子从a点移到c点,质子电势能增加 | |
| B. | 把一电子从b点移到d点,电子电势能增加 | |
| C. | c,d两点电势相等 | |
| D. | a,b两点电势相等 |
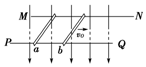 如图所示,两根不计电阻的光滑金属导轨MN、PQ并排固定在同一绝缘水平面上,将两根完全相同的导体棒a、b静止置于导轨上,两棒与导轨接触良好且与导轨垂直,整个装置处于竖直向下的匀强磁场中.已知两导轨间的距离为L,导体棒的质量均为m,现突然给导体棒b一水平瞬间冲量使之产生一向右的初速度v0,下列说法正确的是( )
如图所示,两根不计电阻的光滑金属导轨MN、PQ并排固定在同一绝缘水平面上,将两根完全相同的导体棒a、b静止置于导轨上,两棒与导轨接触良好且与导轨垂直,整个装置处于竖直向下的匀强磁场中.已知两导轨间的距离为L,导体棒的质量均为m,现突然给导体棒b一水平瞬间冲量使之产生一向右的初速度v0,下列说法正确的是( )| A. | 据上述已知量可求出棒a的最终速度 | |
| B. | 据上述已知量可求出通过棒a的最大电量 | |
| C. | 据上述已知量可求出棒a上产生的总焦耳热 | |
| D. | 据上述已知量可求出棒a、b间的最大间距 |
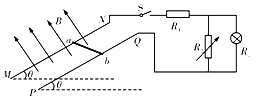 如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面的夹角θ=30°,导轨电阻不计.磁感应强度为B的匀强磁场垂直导轨平面向上,长为L的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m、电阻为R.两金属导轨的上端连接右端电路,灯泡的电阻RL=4R,定值电阻R1=2R,电阻箱电阻调到R2=12R,重力加速度为g,现将金属棒由静止释放,试求:
如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面的夹角θ=30°,导轨电阻不计.磁感应强度为B的匀强磁场垂直导轨平面向上,长为L的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m、电阻为R.两金属导轨的上端连接右端电路,灯泡的电阻RL=4R,定值电阻R1=2R,电阻箱电阻调到R2=12R,重力加速度为g,现将金属棒由静止释放,试求:
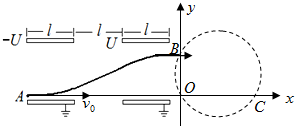 现代科学仪器常利用电场、磁场控制带电粒子的运动.平移器由垂直纸面水平放置的两对平行金属板构成,如图所示.其中极长均为l=0.2m,板间距离均为d=0.3m,两对平行板间的水平间距也为l=0.2m,两极板间偏转电压大小均为U=3×102V,且电场方向相反.平移器右侧有一圆形边界的匀强磁场,磁场方向垂直纸面向外,磁场边界恰好过纸面内坐标系Oxy的坐标原点O且与y轴、x轴相交于B、C两点.现有一质量为m=4×10-10kg、电荷量为q=1×10-6C的带正电粒子以v0=1×103m/s的速度从x轴上的A点射入平移器,且A点恰好在平移器的左边缘,入射方向平行纸面水平向右.粒子离开平移器后恰好从B点进入匀强磁场,并从C点射出磁场,射出磁场时速度方向与x轴正方向的夹角为600,不计粒子重力.求:
现代科学仪器常利用电场、磁场控制带电粒子的运动.平移器由垂直纸面水平放置的两对平行金属板构成,如图所示.其中极长均为l=0.2m,板间距离均为d=0.3m,两对平行板间的水平间距也为l=0.2m,两极板间偏转电压大小均为U=3×102V,且电场方向相反.平移器右侧有一圆形边界的匀强磁场,磁场方向垂直纸面向外,磁场边界恰好过纸面内坐标系Oxy的坐标原点O且与y轴、x轴相交于B、C两点.现有一质量为m=4×10-10kg、电荷量为q=1×10-6C的带正电粒子以v0=1×103m/s的速度从x轴上的A点射入平移器,且A点恰好在平移器的左边缘,入射方向平行纸面水平向右.粒子离开平移器后恰好从B点进入匀强磁场,并从C点射出磁场,射出磁场时速度方向与x轴正方向的夹角为600,不计粒子重力.求: