题目内容
8.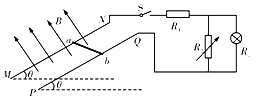 如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面的夹角θ=30°,导轨电阻不计.磁感应强度为B的匀强磁场垂直导轨平面向上,长为L的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m、电阻为R.两金属导轨的上端连接右端电路,灯泡的电阻RL=4R,定值电阻R1=2R,电阻箱电阻调到R2=12R,重力加速度为g,现将金属棒由静止释放,试求:
如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面的夹角θ=30°,导轨电阻不计.磁感应强度为B的匀强磁场垂直导轨平面向上,长为L的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m、电阻为R.两金属导轨的上端连接右端电路,灯泡的电阻RL=4R,定值电阻R1=2R,电阻箱电阻调到R2=12R,重力加速度为g,现将金属棒由静止释放,试求:(1)金属棒下滑的最大速度vm为多大?
(2)当金属棒下滑距离为S0时速度恰达到最大,求金属棒由静止开始下滑2S0的过程中,整个电路产生的电热;
(3)金属杆在加速下滑过程中,当速度达到$\frac{1}{2}$vm时,求此时杆的加速度大小;
(4)改变电阻箱R2的值,当R2为何值时,金属棒达到匀速下滑时R2消耗的功率最大.
分析 (1)金属棒ab先加速下滑,所受的安培力增大,加速度减小,后匀速下滑,速度达到最大.由闭合电路欧姆定律、感应电动势和安培力公式推导出安培力的表达式,根据平衡条件求解最大速度.
(2)当金属棒下滑直到速度达到最大的过程中,金属棒的机械能减小转化为内能,根据能量守恒定律求解电热Q;
(3)根据牛顿第二定律来分析求解加速度大小;
(4)R2消耗的功率P=$\frac{{U}^{2}}{{R}_{2}}$,而U=IR并,金属棒匀速下滑时,重力的功率等于电路的电功率,得到mgsin30°=$\frac{{B}^{2}{d}^{2}v}{3R+{R}_{并}}$,联立得到R2功率P与R2的关系式,由数学知识求最值.
解答 解:(1)当金属棒匀速下滑时速度最大,设最大速度为vm,达到最大时,则根据平衡条件有:
mgsinθ=F安
根据安培力计算公式可得:F安=ILB,
根据闭合电路的欧姆定律可得:I=$\frac{BL{v}_{m}}{{R}_{总}}$
电路总电阻为:R总=R1+R+$\frac{{R}_{2}{R}_{L}}{{R}_{2}+{R}_{L}}$=6R,
解得最大速度vm=$\frac{3mgR}{{B}^{2}{L}^{2}}$;
(2)由能量守恒知:mg•2S0•sinθ=Q+$\frac{1}{2}m{v}_{m}^{2}$,
解得Q=mgs0-$\frac{9{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$;
(3)金属棒速度最大时受力平衡,有mgsinθ=$\frac{{B}^{2}{d}^{2}{v}_{m}}{6R}$
金属棒达到最大速度的一半时受到的安培力大小为FA=$\frac{{B}^{2}{d}^{2}•\frac{1}{2}{v}_{m}}{6R}=\frac{1}{2}mg$,
根据牛顿第二定律可得mgsin30°-FA=ma,
解得:a=$\frac{1}{2}g$;
(4)R2消耗的功率P=$\frac{{U}^{2}}{{R}_{2}}$,而U=IR并=$\frac{{R}_{并}}{{R}_{并}+3R}$BLv,
R并=$\frac{4R{R}_{2}}{4R+{R}_{2}}$
又金属棒匀速运动时,mgsin30°=$\frac{{B}^{2}{d}^{2}v}{3R+{R}_{并}}$
代入得到P=$\frac{(mgsin30°)^{2}}{{B}^{2}{L}^{2}}•\frac{16{R}^{2}{R}_{2}}{(4R+{R}_{2})^{2}}$=$\frac{{m}^{2}{g}^{2}}{4{B}^{2}{L}^{2}}•\frac{16{R}^{2}}{\frac{16{R}^{2}}{{R}_{2}}+8R+{R}_{2}}$
由数学知识得:当$\frac{16{R}^{2}}{{R}_{2}}$=R2时,即R2=4R时,R2消耗的功率P最大,
最大值为Pm=$\frac{{m}^{2}{g}^{2}R}{4{B}^{2}{L}^{2}}$.
答:(1)金属棒下滑的最大速度vm为$\frac{3mgR}{{B}^{2}{L}^{2}}$;
(2)当金属棒下滑距离为S0时速度恰达到最大,求金属棒由静止开始下滑2S0的过程中,整个电路产生的电热为mgs0-$\frac{9{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$;
(3)金属杆在加速下滑过程中,当速度达到$\frac{1}{2}$vm时,此时杆的加速度大小为$\frac{1}{2}g$;
(4)改变电阻箱R2的值,当R2为4R时,金属棒达到匀速下滑时R2消耗的功率最大.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,根据牛顿第二定律或平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | 理想气体对容器的压强是由大量气体分子对容器不断碰撞而产生的 | |
| B. | 若理想气体的内能不变,其状态也一定不变 | |
| C. | 当分子力表现为斥力时,分子力和分子势能总是随分子间距离的减小而增大 | |
| D. | 叶面上的小露珠呈球形是由于液体表面张力的作用 |
 如图所示,A是静止在赤道上的物体,B、C是同一平面内两颗人造卫星.B位于离地高度等于地球半径的圆形轨道上,C是地球同步卫星.则以下判断正确的是( )
如图所示,A是静止在赤道上的物体,B、C是同一平面内两颗人造卫星.B位于离地高度等于地球半径的圆形轨道上,C是地球同步卫星.则以下判断正确的是( )| A. | 卫星B的速度大小等于地球的第一宇宙速度 | |
| B. | A、B的线速度大小关系为vA>vB | |
| C. | 周期大小关系为TA=TC>TB | |
| D. | B、C的线速度大小关系为vc>vB |
| A. | 弹簧的弹性势能最大为$\frac{1}{2}$mv02-Q-fd | |
| B. | 弹簧的弹性势能最大值大于$\frac{1}{2}$mv02-2Q-fd | |
| C. | 导体棒再次回到OO′位置时的动能等于$\frac{1}{2}$mv02-4Q-2fd | |
| D. | 导体棒再次回到OO′位置时的动能大于$\frac{1}{2}$mv02-4Q-2fd |
 如图所示,有四个等量异种电荷,放在正方形的四个顶点处.A、B、C、D为正方形四个边的中点,O为正方形的中心,下列说法中正确的是( )
如图所示,有四个等量异种电荷,放在正方形的四个顶点处.A、B、C、D为正方形四个边的中点,O为正方形的中心,下列说法中正确的是( )| A. | A、C两个点的电场强度方向相反 | |
| B. | O点电场强度等于零 | |
| C. | 将一带正电的试探电荷从B点沿直线移动到D点,电场力做功为零 | |
| D. | O点的电势低于A点的电势 |
| A. | 原子核式结构模型提出的实验基础是α粒子散射实验 | |
| B. | β 射线来自于原子核外电子的电离 | |
| C. | 目前秦山核电站主要利用重核裂变工作 | |
| D. | 光电效应实验中,光电子的最大初动能与入射光的频率成正比 |

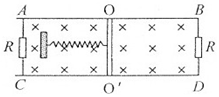
 如图所示,固定的竖直光滑U型金属导轨,间距为L,上端接有阻值为R的电阻,处在方向水平且垂直于导轨平面、磁感应强度为B的匀强磁场中.质量为m、电阻不计的导体棒与劲度系数为k的固定轻弹簧相连放在导轨上,导轨的电阻忽略不计.初始时刻,弹簧处于伸长状态,其伸长量为x1=$\frac{mg}{k}$,此时导体棒具有竖直向下的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.已知重力加速度为g.求:
如图所示,固定的竖直光滑U型金属导轨,间距为L,上端接有阻值为R的电阻,处在方向水平且垂直于导轨平面、磁感应强度为B的匀强磁场中.质量为m、电阻不计的导体棒与劲度系数为k的固定轻弹簧相连放在导轨上,导轨的电阻忽略不计.初始时刻,弹簧处于伸长状态,其伸长量为x1=$\frac{mg}{k}$,此时导体棒具有竖直向下的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.已知重力加速度为g.求: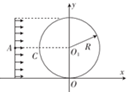 如图所示,x轴正方向水平向右,y轴正方向竖直向上,在xOy平面内存在与y轴平行的匀强电场,圆心在O1(0,R)、半径为R的圆形区域内存在与xOy平面垂直的匀强磁场,在O1的左边垂直x轴放置一微粒发射装置,它可在0<y<2R的范围内沿x轴正方向发射出大量质量均为m、电荷量均为q、初速度均为v的带负电微粒.重力加速度为g.
如图所示,x轴正方向水平向右,y轴正方向竖直向上,在xOy平面内存在与y轴平行的匀强电场,圆心在O1(0,R)、半径为R的圆形区域内存在与xOy平面垂直的匀强磁场,在O1的左边垂直x轴放置一微粒发射装置,它可在0<y<2R的范围内沿x轴正方向发射出大量质量均为m、电荷量均为q、初速度均为v的带负电微粒.重力加速度为g.