��Ŀ����
19��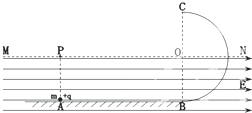 ��ͼ��ʾ���⻬��Եˮƽ�����뾶ΪR�Ĺ⻬��Ե��ֱ��Բ�����B��ƽ�����ӣ��ڹ�Բ��O��ˮƽ������·��ֲ���ˮƽ���ҵ���ǿ�糡������һ������Ϊm������Ϊ+q��С���ˮƽ����ϵ�A���ɾ�ֹ�ͷţ�С���˶���C���뿪Բ���������MN�ϵ�P�����糡��P��ǡ����A������Ϸ���С�����Ϊ�ʵ㣬С���˶������е������ֲ��䣩����֪A��B��ľ���Ϊ2R���������ٶ�Ϊg���������˶������У���
��ͼ��ʾ���⻬��Եˮƽ�����뾶ΪR�Ĺ⻬��Ե��ֱ��Բ�����B��ƽ�����ӣ��ڹ�Բ��O��ˮƽ������·��ֲ���ˮƽ���ҵ���ǿ�糡������һ������Ϊm������Ϊ+q��С���ˮƽ����ϵ�A���ɾ�ֹ�ͷţ�С���˶���C���뿪Բ���������MN�ϵ�P�����糡��P��ǡ����A������Ϸ���С�����Ϊ�ʵ㣬С���˶������е������ֲ��䣩����֪A��B��ľ���Ϊ2R���������ٶ�Ϊg���������˶������У�����1��С����C��ʱ���ٶȣ�
��2���糡ǿ��E�Ĵ�С��
��3��С����Բ������˶�ʱ�Թ�������ѹ����
���� ��1������С����ƽ���˶�����ƽ���˶�ˮƽ��������ٺ���ֱ��������������˶���� ���ɣ�
��2����A��C���ö��ܶ������ ���ɣ�
��3����С���ܵ������͵糡���ĺ���������С���ڹ���ϵ����ѹ��������ţ�ٵڶ�������⼴�ɣ�
��� �⣺��1����C��PС����ƽ���˶�
���ԣ�R=$\frac{1}{2}g{t}^{2}$
2R=vct
�������Ͻ�ã�vc=$\sqrt{2gR}$
��2����A��C�ж��ܶ�����
qE•3R-mg•2R=$\frac{1}{2}mv_c^2$-0
���ԣ�$E=\frac{mg}{q}$
��3������qE=mg������С���˶�����ͼ��ʾ��=45��ʱ�Թ��ѹ�����
����ʱ�Ĺ����С���֧����ΪN���� 
�ݶ��ܶ����ã�qE��2R+Rsin�ȣ�-mg��1-cos�ȣ�=$\frac{1}{2}m{v^2}$-0
��ţ�ٵڶ����ɵã�N-qEsin��-mgcos��=$\frac{{m{v^2}}}{R}$
�������Ͻ�ã�$N=��2+3\sqrt{2}��mg$
����С��Թ�������ѹ��Ϊ$��2+3\sqrt{2}��mg$
��1��С����C��ʱ���ٶ�$\sqrt{2gR}$��
��2���糡ǿ��E�Ĵ�С$\frac{mg}{q}$��
��3��С����Բ������˶�ʱ�Թ�������ѹ����2+$3\sqrt{2}$��mg��
���� ��ȷС����������˶������ǽ���Ĺؼ������Ӧ�ö��ܶ�����ţ�ٵڶ������ǽ���Ĺؼ�����Ŀ�ۺ��Խ�ǿ��

 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�| A�� | �������������������е�����Ϊ2��$\sqrt{\frac{R}{g}}$ | |
| B�� | �ڷ����������Ĺ�����������������ٶ�Ϊ��$\frac{R}{R+h}$��2g | |
| C�� | �����������ڹ�������ϵ������ٶ�Ϊ$\sqrt{g��R+h��}$ | |
| D�� | ����Ŀ������֪�����ƽ���ܶ�Ϊ$\frac{3g}{4��GR}$ |
 ��ͼ��ʾΪa��b��С���ع⻬ˮƽ�������˶���v-tͼ����֪��С����С�ڻ����Lʱ���ܵ���ų�������ã���������Lʱ�����������Ϊ�㣮��ͼ��֪��������
��ͼ��ʾΪa��b��С���ع⻬ˮƽ�������˶���v-tͼ����֪��С����С�ڻ����Lʱ���ܵ���ų�������ã���������Lʱ�����������Ϊ�㣮��ͼ��֪��������| A�� | a�������С��b������� | |
| B�� | t1ʱ����������С | |
| C�� | 0��t2������������t2��t4�������������� | |
| D�� | t2��t3�������λ�Ʋ�С��L |
| A�� | F | B�� | 2F | C�� | $\frac{F}{2}$ | D�� | $\frac{F}{4}$ |
| A�� | ���������ĵ����һ����1.6��10-19C | |
| B�� | ������ָ���ӡ�������Щ������ | |
| C�� | ����������ģ�� | |
| D�� | ������ָ�������С�Ĵ����� |
 ����Ϊ0.3kg��������ˮƽ������ֱ���˶���ͼ�е�����ֱ�߷ֱ��ʾ������ˮƽ�����Ͳ���ˮƽ������ͼ�ߣ�������˵����ȷ���ǣ�������
����Ϊ0.3kg��������ˮƽ������ֱ���˶���ͼ�е�����ֱ�߷ֱ��ʾ������ˮƽ�����Ͳ���ˮƽ������ͼ�ߣ�������˵����ȷ���ǣ�������| A�� | ˮƽ����������0.3 N | B�� | ˮƽ����һ����0.1 N | ||
| C�� | ��������Ħ����һ����0.1N | D�� | ��������Ħ����һ����0.2 N |
 ��ͼ��ʾ��EF��GH��Ϊһ�������������A��BΪ���Ϊd���峤ΪL��ˮƽ���õ�ƽ�н����壬�����ϼ�ijһ��ѹ�Ӷ��ڰ���γ�һ��ǿ�糡������AΪ�����壮�����Ҳ�Ϊһ��ֱ��ֽ�����ǿ�ų���OΪԲ���ξ�ԵϸԲ��CD��Բ�ģ�Բ���뾶ΪR��Բ�Ľ�Ϊ120�㣬O��C���������������ϣ�Dλ��GH�ϣ�һ������Ϊm�������Ϊq�Ĵ����������Գ��ٶ�v0��������������������ǿ�糡�����ӳ���ǿ�糡��������ǡ����Բ�����߷������ϸԲ�ܣ�������ܱ������ѹ�뾶ΪR������Բ���˶������������ӵ��������ܵĴ�ϸ����
��ͼ��ʾ��EF��GH��Ϊһ�������������A��BΪ���Ϊd���峤ΪL��ˮƽ���õ�ƽ�н����壬�����ϼ�ijһ��ѹ�Ӷ��ڰ���γ�һ��ǿ�糡������AΪ�����壮�����Ҳ�Ϊһ��ֱ��ֽ�����ǿ�ų���OΪԲ���ξ�ԵϸԲ��CD��Բ�ģ�Բ���뾶ΪR��Բ�Ľ�Ϊ120�㣬O��C���������������ϣ�Dλ��GH�ϣ�һ������Ϊm�������Ϊq�Ĵ����������Գ��ٶ�v0��������������������ǿ�糡�����ӳ���ǿ�糡��������ǡ����Բ�����߷������ϸԲ�ܣ�������ܱ������ѹ�뾶ΪR������Բ���˶������������ӵ��������ܵĴ�ϸ����