题目内容
9.探月工程三期飞行试验器于2014年10月24日2时在中国西昌卫星发射中心发射升窄,飞行试验器飞抵距月球6万千米附近进入月球引力影响区,开始月球近旁转向飞行,最终进入距月球表面h=200km的圆形工作轨道.设月球半径为R,月球表面的重力加速度为g,万有引力常量为G,则下列说法正确的是( )| A. | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| B. | 在飞行试验器的工作轨道处的重力加速度为($\frac{R}{R+h}$)2g | |
| C. | 飞行试验器在工作轨道上的绕行速度为$\sqrt{g(R+h)}$ | |
| D. | 由题目条件可知月球的平均密度为$\frac{3g}{4πGR}$ |
分析 根据万有引力提供向心力,推导出线速度和角速度及周期的公式,得出选项.
解答 解:AC、根据万有引力提供向心力,即:$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m\frac{4{π}^{2}}{{T}^{2}}r$,解得:$v=\sqrt{\frac{GM}{r}}$,$T=2π\sqrt{\frac{{r}^{3}}{GM}}$
飞行试验器的轨道半径为r=R+h,结合黄金代换公式:GM=gR2,代入线速度和周期公式得:$v=\sqrt{\frac{{R}^{2}g}{R+h}}$,$T=2π\sqrt{\frac{(R+h)^{3}}{g{R}^{2}}}$,故AC错误;
D、由黄金代换公式得中心天体的质量$M=\frac{g{R}^{2}}{G}$,月球的体积$V=\frac{4}{3}π{R}^{3}$,则月球的密度$ρ=\frac{3g}{4πGR}$,故D正确;
B、月球表面万有引力等于重力,则$G\frac{Mm}{(R+h)^{2}}=mg′$,得:$g′=(\frac{R}{R+h})^{2}g$,故B正确;
故选:BD
点评 本题关键根据卫星的万有引力等于向心力,以及星球表面重力等于万有引力列两个方程求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.一个力作用于质量为m1的物体A时,加速度为a1;这个力作用于质量为m2的物体时,加速度为a2,如果这个力作用于质量为m1+m2的物体C时,得到的加速度为( )
| A. | $\frac{{a}_{1}+{a}_{2}}{2}$ | B. | $\frac{{m}_{1}{a}_{1}}{{m}_{1}+{m}_{2}}$ | C. | $\frac{{m}_{2}{a}_{2}}{{m}_{1}+{m}_{2}}$ | D. | $\frac{{a}_{1}{a}_{2}}{{a}_{1}+{a}_{2}}$ |
17.如图甲所示,一个弹簧一端固定在传感器上,传感器与电脑相连,当对弹簧施加变化的作用力(拉力或压力)时,在电脑上得到了弹簧长度的形变量与弹簧产生的弹力大小的关系图象(如图乙).则下列判断正确的是( )
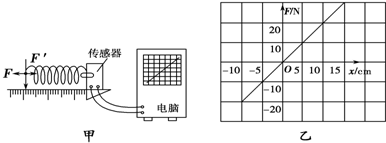

| A. | 弹簧产生的弹力和弹簧的长度成正比 | |
| B. | 弹簧长度的增加量与对应的弹力增加量成正比 | |
| C. | 该弹簧的劲度系数是200 N/m | |
| D. | 该弹簧受到反向压力时,劲度系数不变 |
4.用如图1所示的实验装置探究加速度与力、质量的关系
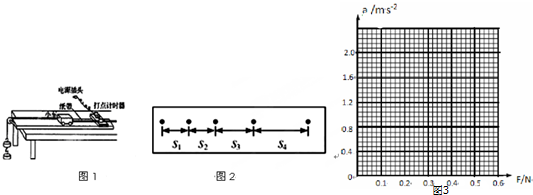
(1)图2是实验中得到的一条纸带,相邻计数点间的时间间隔是t.测出纸带各相邻计数点之间的距离分别为s1、s2、s3、s4,为使由实验数据计算的结果更精确一些,计算加速度公式应为a=$\frac{{{s}_{4}+s}_{3}-{s}_{2}-{s}_{1}}{4{t}^{2}}$
(2)某同学在该实验中得到如下一组实验数据(表中F表示细线对小车的拉力,a表示小车的加速度):
①如图3示,请在答题纸相应的图中中作出a-F图象
②根据图表分析,实验操作中存在的问题可能是A
A.平衡摩擦力时木板倾角过小
B.平衡摩擦力时木板倾角过大
C.小车质量太大
D.钩码的质量太大.

(1)图2是实验中得到的一条纸带,相邻计数点间的时间间隔是t.测出纸带各相邻计数点之间的距离分别为s1、s2、s3、s4,为使由实验数据计算的结果更精确一些,计算加速度公式应为a=$\frac{{{s}_{4}+s}_{3}-{s}_{2}-{s}_{1}}{4{t}^{2}}$
(2)某同学在该实验中得到如下一组实验数据(表中F表示细线对小车的拉力,a表示小车的加速度):
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/m•s-2 | 0.25 | 0.57 | 0.89 | 1.20 | 1.52 |
②根据图表分析,实验操作中存在的问题可能是A
A.平衡摩擦力时木板倾角过小
B.平衡摩擦力时木板倾角过大
C.小车质量太大
D.钩码的质量太大.
1.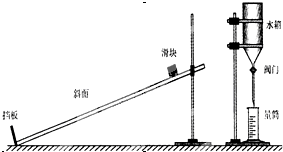 伽利略在《两种新科学的对话》一书中,讨论了自由落体运动和物体沿斜面运动的问题,提出了这样的猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还运用实验验证了其猜想.某校物理兴趣小组依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.
伽利略在《两种新科学的对话》一书中,讨论了自由落体运动和物体沿斜面运动的问题,提出了这样的猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还运用实验验证了其猜想.某校物理兴趣小组依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.
(1)实验时,让滑块从不同高度由静止沿斜面下滑,并同时打开装置中的阀门,使水箱中的水流到量筒中;当滑块碰到挡板的同时关闭阀门(整个过程中水流可视为均匀稳定的).该实验探究方案是利用量筒中收集的水量来测量时间的. 水滴下落时间与等高物体运动时间不相等(填“相等”或“不相等”)
(2)表是该小组测得的有关数据,s为滑块从斜面的不同高度由静止释放后沿斜面下滑的距离,V为相应过程量筒收集的水量.分析表中数据,根据误差允许范围内,$\frac{S}{{V}^{2}}$为定值,可以得出滑块沿斜面下滑是做匀变速直线运动的结论.
 伽利略在《两种新科学的对话》一书中,讨论了自由落体运动和物体沿斜面运动的问题,提出了这样的猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还运用实验验证了其猜想.某校物理兴趣小组依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.
伽利略在《两种新科学的对话》一书中,讨论了自由落体运动和物体沿斜面运动的问题,提出了这样的猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还运用实验验证了其猜想.某校物理兴趣小组依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.(1)实验时,让滑块从不同高度由静止沿斜面下滑,并同时打开装置中的阀门,使水箱中的水流到量筒中;当滑块碰到挡板的同时关闭阀门(整个过程中水流可视为均匀稳定的).该实验探究方案是利用量筒中收集的水量来测量时间的. 水滴下落时间与等高物体运动时间不相等(填“相等”或“不相等”)
(2)表是该小组测得的有关数据,s为滑块从斜面的不同高度由静止释放后沿斜面下滑的距离,V为相应过程量筒收集的水量.分析表中数据,根据误差允许范围内,$\frac{S}{{V}^{2}}$为定值,可以得出滑块沿斜面下滑是做匀变速直线运动的结论.
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| S(m) | 4.5 | 3.9 | 3.0 | 2.1 | 1.5 | 0.9 | 0.3 |
| V(mL) | 90 | 84 | 72 | 62 | 52 | 40 | 23.5 |
| $\frac{S}{{V}^{2}}$×10-4 | 5.6 | 5.5 | 5.8 | 5.5 | 5.6 | 5.6 | 5.4 |
18.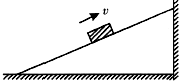 如图所示,质量为M的斜劈靠墙放置,质量为m的滑块以一定的初速度滑上斜劈,只考虑滑块与斜面间的摩擦,不计其它接触面之间的摩擦,则在滑块上滑的过程中( )
如图所示,质量为M的斜劈靠墙放置,质量为m的滑块以一定的初速度滑上斜劈,只考虑滑块与斜面间的摩擦,不计其它接触面之间的摩擦,则在滑块上滑的过程中( )
 如图所示,质量为M的斜劈靠墙放置,质量为m的滑块以一定的初速度滑上斜劈,只考虑滑块与斜面间的摩擦,不计其它接触面之间的摩擦,则在滑块上滑的过程中( )
如图所示,质量为M的斜劈靠墙放置,质量为m的滑块以一定的初速度滑上斜劈,只考虑滑块与斜面间的摩擦,不计其它接触面之间的摩擦,则在滑块上滑的过程中( )| A. | 地面对斜劈的支持力大于(M+m)g | B. | 地面对斜劈的支持力小于(M+m)g | ||
| C. | 墙壁对斜劈的弹力大小在逐渐减小 | D. | 墙壁对斜劈的弹力大小始终不变 |
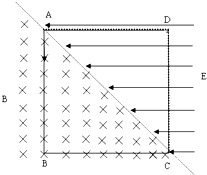 如图所示,在边长为a的正方形ABCD的对角线AC左右两侧,分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场,AD、CD是两块固定荧光屏(能吸收打到屏上的粒子).现有一群质量为m、电量为q的带正电粒子,从A点沿AB方向以不同速率连续不断地射入匀强磁场中,带电粒子速率范围为$\frac{aqB}{12cm}$≤v≤$\frac{aq{B}^{2}}{m}$.已知E=$\frac{aq{B}^{2}}{12m}$,不计带电粒子的重力和粒子之间的相互作用.求:
如图所示,在边长为a的正方形ABCD的对角线AC左右两侧,分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场,AD、CD是两块固定荧光屏(能吸收打到屏上的粒子).现有一群质量为m、电量为q的带正电粒子,从A点沿AB方向以不同速率连续不断地射入匀强磁场中,带电粒子速率范围为$\frac{aqB}{12cm}$≤v≤$\frac{aq{B}^{2}}{m}$.已知E=$\frac{aq{B}^{2}}{12m}$,不计带电粒子的重力和粒子之间的相互作用.求: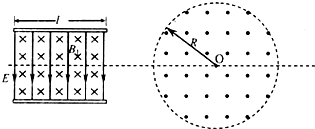
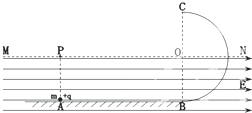 如图所示,光滑绝缘水平轨道与半径为R的光滑绝缘竖直半圆轨道在B点平滑连接.在过圆心O的水平界面的下方分布有水平向右的匀强电场.现有一个质量为m、电量为+q的小球从水平轨道上的A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方,小球可视为质点,小球运动过程中电量保持不变).已知A、B间的距离为2R,重力加速度为g,在上述运动过程中,求:
如图所示,光滑绝缘水平轨道与半径为R的光滑绝缘竖直半圆轨道在B点平滑连接.在过圆心O的水平界面的下方分布有水平向右的匀强电场.现有一个质量为m、电量为+q的小球从水平轨道上的A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方,小球可视为质点,小球运动过程中电量保持不变).已知A、B间的距离为2R,重力加速度为g,在上述运动过程中,求: