甲.乙.丙三个小球分别位于如图所示的竖直平面内.甲.乙在同一条竖直线上.甲.丙在同一条水平线上.水平面上的P点在丙的正下方.在同一时刻甲.乙.丙开始运动.甲以水平速度v0做平抛运动.乙以水平速度v0沿水平面向右做匀速直线运动.丙做自由落体运动．则下列说法错误的是( )A．若甲.乙.丙三球同时相遇.则一定发生在P点B．若甲.丙二球在空中相遇.此时乙球一题目和参考答案——青夏教育精英家教网—

题目内容

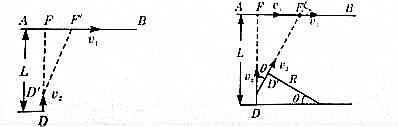
18．

甲、乙、丙三个小球分别位于如图所示的竖直平面内，甲、乙在同一条竖直线上，甲、丙在同一条水平线上，水平面上的P点在丙的正下方，在同一时刻甲、乙、丙开始运动，甲以水平速度v₀做平抛运动，乙以水平速度v₀沿水平面向右做匀速直线运动，丙做自由落体运动．则下列说法错误的是（　　）

	A．	若甲、乙、丙三球同时相遇，则一定发生在P点
	B．	若甲、丙二球在空中相遇，此时乙球一定在P点
	C．	若甲与丙距离足够大，则丙球一定先落地
	D．	任意时刻甲、乙的水平位移一定相同

分析平抛运动在水平方向做匀速直线运动，竖直方向上做自由落体运动，两个分运动具有等时性．结合平抛运动的规律分析判断．

解答解：A、甲做平抛运动，在水平方向上做匀速直线运动，所以在在未落地前任何时刻，甲乙两球都在一竖直线上，最后在地面上相遇，可能在P点前，也可能在P点后；甲在竖直方向上做自由落体运动，所以在未落地前的任何时刻，甲丙两球在同一水平线上，两球相遇点可能在空中，可能在P点．所以，若三球同时相遇，则一定在P点，故A正确．
B、若甲丙两球在空中相遇，由于甲乙两球在甲未落地前，始终在同一竖直线上，可知此时乙球一定在P点，故B正确．
C、由于甲在竖直方向上做自由落体运动，可知甲丙两球一定同时落地，故C错误．
D、甲乙在水平方向上的运动规律相同，在任意时刻甲乙的水平位移一定相同，故D正确．
本题选错误的，故选：C．

点评解决本题的关键掌握处理平抛运动的方法，在水平方向上做匀速直线运动，在竖直方向上做自由落体运动．

练习册系列答案

相关题目

3．

如图所示，在溜冰场上经常看到，两人面对面拉着做圆周运动的表演，假设某光滑的溜冰场上，有甲、乙两名溜冰爱好者，m_甲=80kg，m_乙=40kg，面对面拉着水平的弹簧测力计做圆周运动的溜冰表演，两人相距0.9m，弹簧秤的示数为96N．求
（1）两人的运动半径r_甲和r_乙；
（2）两人的角速度ω_甲和ω_乙；
（3）两人的线速度v_甲和v_乙．

9．

如图所示，支架装置BO′O可绕竖直轴O′O水平转动，可视为质点的小球A与两细线连接后分别系于B、C两点，装置静止时细线AB水平，细线AC与竖直方向的夹角为37°．已知小球的质量m=1kg，细线AC长L=lm，B点距转轴O′O的水平距离和距C点竖直距离相等．（重力加速度g取l0m/m²．sin37°=0.6．cos37°=0.8．sm53°=0.8，cos53°=0.6）
（1）若装罝静止不动时，求细线AB的拉力T_B和细线AC的拉力T_C的大小；
（2）若装置以角速度ω=2$\sqrt{5}$rad/s绕竖直轴O′O水平匀速转动时，求细线AC和转轴O′O间夹角θ的大小？

6．用如图1所示的实验装置验证m₁、m₂组成的系统机械能守恒．m₂从高处由静止开始下落，m₁上拖着的纸带打出一系列的点，对纸带上的点迹进行测量，即可验证机械能守恒．图2给出的是实验中获取的一条纸带；0是打下的第一个点，每相邻两个计数点点间还有4个点（图中未标出），计数点间的距离如图2所示．已知两个物体m₁=100g、m₂=300g，则（g=9.8m/s²）
（1）在纸带上打下计数点5时的速度v=2.4m/s；
（2）在打点0-5过程中系统动能的增加量△E_k=1.15J，系统重力势能的减少量△E_p=1.18J，由此得出的结论是在误差允许的范围内，系统的系统机械能守恒；（结果保留三位有效数字）
（3）若某同学作出$\frac{{v}^{2}}{2}$-h图象如图3所示，则根据图象求得的重力加速度g=5.76m/s²．

13．

用图示的方法可以测出一个人的反应时间，甲同学用手握住直尺顶端刻度为零的地方，乙同学在直尺下端刻度a的地方做捏住直尺的准备，但手没有碰直尺．当乙同学看到甲同学放开直尺时，立即握住直尺，结果乙同学握住直尺的刻度为b，已知重力加速度为g，则乙同学的反应时间为（　　）

A．

$\sqrt{\frac{2a}{g}}$

B．

$\sqrt{\frac{2b}{g}}$

C．

$\sqrt{\frac{2（a-b）}{g}}$

D．

$\sqrt{\frac{2（b-a）}{g}}$

3．

如图所示，ABCD是厚度为d的圆柱形玻璃体截面．厚度不计、半径为r的圆形LED灯贴在玻璃体CD面上，圆心与CD面中心P重合，其发出的光从AB面射出，玻璃的折射率为$\sqrt{2}$．不考虑光在AD和BC面上的反射，要使光从AB面射出的角度范围为180°，求玻璃体的最小半径R．

10．在某星球表面，用弹簧测力计测得质量为m₀的物体的重力为P，已知该星球的半径为R，万有引力常量为G，它的同步通讯卫星的轨道离地面的高度为h，则（　　）

	A．	星球的质量为$\frac{P{R}^{2}}{G{m}_{0}}$
	B．	星球的同步通讯卫星环绕地球运动的向心加速度大小等于$\frac{P}{{m}_{0}}$
	C．	星球的自转周期等于$\frac{2π}{R}$$\sqrt{\frac{{m}_{0}（R+h）^{3}}{P}}$
	D．	该星球的第一宇宙速度为v=R$\sqrt{\frac{P}{{m}_{0}}}$

7．一只狐狸以不变的速度v₁沿直线AB逃跑，一猎犬以不变的速率v₂追击，其运动方向始终对准狐理．某时刻狐狸在F处，猎犬在D处，FD⊥AB，且FD=L，求：
（1）此时猎犬加速度的大小，
（2）猎犬追上狐狸需要多长时间？

6．火车通过弯道时，为了保证安全，要求火车在按规定速度行驶时内外侧轨道均不向车施加侧向力，假设火车在某转弯处的规定行驶速度为v，则下列说法正确的是（　　）

	A．	当火车以速度V通过此转弯处时，所受到的重力及铁轨对火车的支持力这两个力的合力提供了转弯的向心力
	B．	当火车以速度V通过次弯道，受到重力、铁轨的支持力和转弯的向心力作用
	C．	当火车以大于V的速度通过此转弯处时，车轮轮缘会挤压外轨
	D．	当火车以大于V的速度通过此转弯处时，车轮轮缘会挤压内轨

试题分类