题目内容
2.通过观察冥王星的卫星,可以推算出冥王星的质量.假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量.这两个物理量可以是( )| A. | 卫星的速度和角速度 | B. | 卫星的质量和轨道半径 | ||
| C. | 卫星的质量和角速度 | D. | 卫星的运行周期和轨道半径 |
分析 人造卫星绕地球做匀速圆周运动时,万有引力充当向心力,由万有引力定律结合牛顿第二定律列式求中心天体的质量,然后由选项条件判断正确的答案.
解答 解:卫星围绕冥王星做匀速圆周运动,万有引力提供向心力,
A、已知卫星的速度和角速度,则轨道半径r=$\frac{v}{ω}$,根据$G\frac{Mm}{{r}^{2}}=mωv$即可求解冥王星质量M,故A正确;
B、根据$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$可知,卫星的质量可以约去,只知道半径不能求出冥王星质量,故B错误;
C、根据$G\frac{Mm}{{r}^{2}}=m{ω}^{2}r$可知,卫星的质量可以约去,只知道角速度不能求出冥王星质量,故C错误;
D、根据$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$可知,知道卫星的运行周期和轨道半径可求解冥王星质量M,故D正确;
故选:AD
点评 解答万有引力定律在天体运动中的应用时要明确天体做匀速圆周运动,其受到的万有引力提供向心力,会用线速度、角速度、周期表示向心力,同时注意公式间的化简.

练习册系列答案
相关题目
13.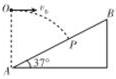 如图所示.一质量为1kg的小球自斜面底端A点正上方O点以v0=4m/s水平抛出,击中斜面上的P点,己知OA之间的距离为8m,g=10m/s2.则( )
如图所示.一质量为1kg的小球自斜面底端A点正上方O点以v0=4m/s水平抛出,击中斜面上的P点,己知OA之间的距离为8m,g=10m/s2.则( )
 如图所示.一质量为1kg的小球自斜面底端A点正上方O点以v0=4m/s水平抛出,击中斜面上的P点,己知OA之间的距离为8m,g=10m/s2.则( )
如图所示.一质量为1kg的小球自斜面底端A点正上方O点以v0=4m/s水平抛出,击中斜面上的P点,己知OA之间的距离为8m,g=10m/s2.则( )| A. | 小球在空中飞行的时间为2s | |
| B. | 小球到达P点时速度为10 m/s | |
| C. | 小球到达P点时重力的功率为100W | |
| D. | 小球整个运动过程中速度的增加量为(2$\sqrt{29}$-4)m/s |
17. 如图是用自由落体法验证机械能守恒定律时得到的一条纸带,有关尺寸已在图中注明,取n点来验证机械能守恒定律,下面列举一些计算n点速度的方法,其中正确的是( )
如图是用自由落体法验证机械能守恒定律时得到的一条纸带,有关尺寸已在图中注明,取n点来验证机械能守恒定律,下面列举一些计算n点速度的方法,其中正确的是( )
 如图是用自由落体法验证机械能守恒定律时得到的一条纸带,有关尺寸已在图中注明,取n点来验证机械能守恒定律,下面列举一些计算n点速度的方法,其中正确的是( )
如图是用自由落体法验证机械能守恒定律时得到的一条纸带,有关尺寸已在图中注明,取n点来验证机械能守恒定律,下面列举一些计算n点速度的方法,其中正确的是( )| A. | n点是第n个点,则vn=gnT | B. | n点是第n个点,则vn=g(n-1)T | ||
| C. | vn=$\frac{{x}_{n}+{x}_{n+1}}{2T}$ | D. | vn=$\frac{{h}_{n+1}-{h}_{n-1}}{2T}$ |
16.下列物理量中属于矢量的是( )
| A. | 功 | B. | 时间 | C. | 电场强度 | D. | 动能 |
17.液体与固体接触的位置会形成液体附着层,使得水在玻璃试管中的液面与器壁接触的位置向下弯曲,水银在玻璃试管中的液面与器壁接触的位置向上弯曲.关于上述现象,下列说法正确的是( )
| A. | 水附着层的分子比内部密集,表现为浸润 | |
| B. | 水附着层的分子比内部稀疏,表现为浸润 | |
| C. | 水银附着层的分子比内部密集,表现为浸润 | |
| D. | 水银附着层的分子比内部稀疏,表现为不浸润 |
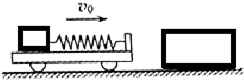 如图,水平面上有一质量m=10kg 的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=10kg 的小物块,小物块与小车一起以v0=6m/s 的速度向右运动,与静止在水平面上质量M=40kg 的木箱发生正碰,碰后木箱的速度为v=2m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力.求:
如图,水平面上有一质量m=10kg 的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=10kg 的小物块,小物块与小车一起以v0=6m/s 的速度向右运动,与静止在水平面上质量M=40kg 的木箱发生正碰,碰后木箱的速度为v=2m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力.求: 如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为$\frac{\sqrt{3}}{3}$mg. 在改变电场强度的大小和方向后,小球A的平衡位置在α=60°处,然后再将A的质量改变为2m,其新的平衡位置在α=30°处,A受到的电场力大小为mg.
如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为$\frac{\sqrt{3}}{3}$mg. 在改变电场强度的大小和方向后,小球A的平衡位置在α=60°处,然后再将A的质量改变为2m,其新的平衡位置在α=30°处,A受到的电场力大小为mg.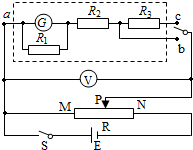 某同学改装和校准电压表的电路图如图所示,图中虚线框内是电压表的改装电路.
某同学改装和校准电压表的电路图如图所示,图中虚线框内是电压表的改装电路. 对改装表3V挡的不同刻度进行校准.所用电池的电动势E为5V;滑动变阻器R有两种规格,最大阻值分别为50Ω和5kΩ.为了方便实验中调节电压,图中R应选用最大阻值为50Ω的滑动变阻器.
对改装表3V挡的不同刻度进行校准.所用电池的电动势E为5V;滑动变阻器R有两种规格,最大阻值分别为50Ω和5kΩ.为了方便实验中调节电压,图中R应选用最大阻值为50Ω的滑动变阻器. 如图,物块A通过一不可伸长的轻绳悬挂在天花板下,初始时静止;从发射器(图中未画出)射出的物块B沿水平方向与A相撞,碰撞后两者粘连在一起运动,碰撞前B的速度的大小v及碰撞后A和B一起上升的高度h均可由传感器(图中未画出)测得.某同学以h为纵坐标,v2为横坐标,利用实验数据作直线拟合,求得该直线的斜率为k=1.92×10-3s2/m.已知物块A和B的质量分别为mA=0.400kg和mB=0.100kg,重力加速度大小g=9.8m/s2.
如图,物块A通过一不可伸长的轻绳悬挂在天花板下,初始时静止;从发射器(图中未画出)射出的物块B沿水平方向与A相撞,碰撞后两者粘连在一起运动,碰撞前B的速度的大小v及碰撞后A和B一起上升的高度h均可由传感器(图中未画出)测得.某同学以h为纵坐标,v2为横坐标,利用实验数据作直线拟合,求得该直线的斜率为k=1.92×10-3s2/m.已知物块A和B的质量分别为mA=0.400kg和mB=0.100kg,重力加速度大小g=9.8m/s2.