题目内容
12.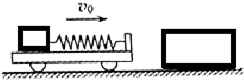 如图,水平面上有一质量m=10kg 的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=10kg 的小物块,小物块与小车一起以v0=6m/s 的速度向右运动,与静止在水平面上质量M=40kg 的木箱发生正碰,碰后木箱的速度为v=2m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力.求:
如图,水平面上有一质量m=10kg 的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=10kg 的小物块,小物块与小车一起以v0=6m/s 的速度向右运动,与静止在水平面上质量M=40kg 的木箱发生正碰,碰后木箱的速度为v=2m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力.求:(1)小车与木箱碰撞后瞬间小车的速度v1;
(2)从碰后瞬间到弹簧被压缩至最短的过程中,弹簧弹力对小车的冲量大小及弹簧弹性势能的最大值.
分析 (1)小车与木箱碰撞过程满足动量守恒定律,由动量守恒定律求小车与木箱碰撞后瞬间小车的速度v1;
(2)弹簧被压缩至最短时,小物块与小车的速度相同.根据动量守恒定律求出共同速度.对小车,运用动量定理求弹簧弹力对小车的冲量大小,由能量守恒定律求弹.簧弹性势能的最大值.
解答 解;(1)小车与木箱碰撞过程,取向右为正方向,由动量守恒定律有
mv0=Mv+mv1
解得:v1=-2 m/s,负号表示碰撞后小车向左运动
(2)当弹簧被压缩到最短时,设小车的速度大小为v2,根据动量守恒定律有:
m0v0+mv1=(m0+m)v2
解得:v2=2 m/s
设碰撞后到弹簧最短的过程,弹簧弹力对小车的冲量大小为I,根据动量定理有:
I=mv2-mv1
解得:I=40N•s
弹性势能的最大值:$\frac{1}{2}$mm0v02+$\frac{1}{2}$mv12=$\frac{1}{2}$(m0+m)v22+Epm
解得:Epm =160J
答:
(1)小车与木箱碰撞后瞬间小车的速度v1大小为2 m/s,方向向左.
(2)从碰后瞬间到弹簧被压缩至最短的过程中,弹簧弹力对小车的冲量大小是40N•s,弹簧弹性势能的最大值是160J.
点评 本题在整个运动的过程中,系统的动量守恒,对于不同的过程,根据动量守恒定律和能量守恒定律计算即可,注意要规定正方向.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3. 如图,A为静止于地球赤道上的物体、B为近地卫星、C为地球同步卫星,地球表面的重力加速度为g,关于它们运行线速度v、角速度ω、周期T和加速度a的比较正确的是( )
如图,A为静止于地球赤道上的物体、B为近地卫星、C为地球同步卫星,地球表面的重力加速度为g,关于它们运行线速度v、角速度ω、周期T和加速度a的比较正确的是( )
 如图,A为静止于地球赤道上的物体、B为近地卫星、C为地球同步卫星,地球表面的重力加速度为g,关于它们运行线速度v、角速度ω、周期T和加速度a的比较正确的是( )
如图,A为静止于地球赤道上的物体、B为近地卫星、C为地球同步卫星,地球表面的重力加速度为g,关于它们运行线速度v、角速度ω、周期T和加速度a的比较正确的是( )| A. | TA=TC>TB | B. | vA>vB>vC | C. | aB=g>aC>aA | D. | ωA>ωB>ωC |
20. 如图所示,a,b为两束不同频率的单色光,以45°的入射角到玻璃砖的上表面,直线OO′与玻璃砖垂直且与其上表面交于N点,入射点A、B到N点的距离相等,经玻璃砖上表面折射后两束光相交于图中的P点.下列说法正确的是( )
如图所示,a,b为两束不同频率的单色光,以45°的入射角到玻璃砖的上表面,直线OO′与玻璃砖垂直且与其上表面交于N点,入射点A、B到N点的距离相等,经玻璃砖上表面折射后两束光相交于图中的P点.下列说法正确的是( )
 如图所示,a,b为两束不同频率的单色光,以45°的入射角到玻璃砖的上表面,直线OO′与玻璃砖垂直且与其上表面交于N点,入射点A、B到N点的距离相等,经玻璃砖上表面折射后两束光相交于图中的P点.下列说法正确的是( )
如图所示,a,b为两束不同频率的单色光,以45°的入射角到玻璃砖的上表面,直线OO′与玻璃砖垂直且与其上表面交于N点,入射点A、B到N点的距离相等,经玻璃砖上表面折射后两束光相交于图中的P点.下列说法正确的是( )| A. | a光在玻璃砖中的折射率大于b光在玻璃砖中的折射率 | |
| B. | 在玻璃中,a光的传播速度大于b光的传播速度 | |
| C. | 增大入射角(入射角始终小于90°),则a光在玻璃砖的下表面先发生全反射 | |
| D. | 对同一双缝干涉装置,a光的干涉条纹比b光的干涉条纹间距大 |
7.某同学为了测定某电源的电动势E和内阻r以及一段电阻丝的电阻率ρ,设计了如图(a)所示的电路.ab是一段电阻率较大的粗细均匀的电阻丝,R0是阻值为2Ω的保护电阻,滑动片P与电阻丝接触始终良好.实验时闭合电键,调节P的位置,将aP长度x和对应的电压U、电流I数据记录如下表:

(1)该同学根据实验数据绘制了如图(b)所示的U-I图象,可得电源的电动势E=3.0V;内阻 r=1Ω.
(2)请你根据表中数据在图(c)上描点连线作$\frac{U}{I}$和x关系图线.
(3)已知金属丝的横截面积s=0.12×10-6m2,利用图(c)图线,可以求得电阻丝的电阻率ρ为1.2×10-6Ω(保留两位有效数字);根据图(c)图线还可以得到的信息是电流表的内阻为2.0Ω.
| x(m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| U(V) | 1.50 | 1.72 | 1.95 | 2.00 | 2.10 | 2.18 |
| I(A) | 0.49 | 0.43 | 0.38 | 0.33 | 0.31 | 0.28 |
| U/I(Ω) | 3.06 | 4.00 | 5.13 | 6.06 | 6.77 | 7.79 |

(1)该同学根据实验数据绘制了如图(b)所示的U-I图象,可得电源的电动势E=3.0V;内阻 r=1Ω.
(2)请你根据表中数据在图(c)上描点连线作$\frac{U}{I}$和x关系图线.
(3)已知金属丝的横截面积s=0.12×10-6m2,利用图(c)图线,可以求得电阻丝的电阻率ρ为1.2×10-6Ω(保留两位有效数字);根据图(c)图线还可以得到的信息是电流表的内阻为2.0Ω.
1. 如图所示,某同学对着墙壁练习打乒乓球,某次球与墙壁上A点碰撞后水平弹离,恰好垂直落在球拍上的B点,已知球拍与水平方向夹角θ=60°,AB两点高度差h=1m,忽略空气阻力,重力加速度g=10m/s2,则球刚要落到球拍上时速度大小为( )
如图所示,某同学对着墙壁练习打乒乓球,某次球与墙壁上A点碰撞后水平弹离,恰好垂直落在球拍上的B点,已知球拍与水平方向夹角θ=60°,AB两点高度差h=1m,忽略空气阻力,重力加速度g=10m/s2,则球刚要落到球拍上时速度大小为( )
 如图所示,某同学对着墙壁练习打乒乓球,某次球与墙壁上A点碰撞后水平弹离,恰好垂直落在球拍上的B点,已知球拍与水平方向夹角θ=60°,AB两点高度差h=1m,忽略空气阻力,重力加速度g=10m/s2,则球刚要落到球拍上时速度大小为( )
如图所示,某同学对着墙壁练习打乒乓球,某次球与墙壁上A点碰撞后水平弹离,恰好垂直落在球拍上的B点,已知球拍与水平方向夹角θ=60°,AB两点高度差h=1m,忽略空气阻力,重力加速度g=10m/s2,则球刚要落到球拍上时速度大小为( )| A. | 2$\sqrt{5}$m/s | B. | 2$\sqrt{15}$m/s | C. | 4$\sqrt{5}$m/s | D. | $\frac{4}{3}$$\sqrt{15}$m/s |
2.通过观察冥王星的卫星,可以推算出冥王星的质量.假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量.这两个物理量可以是( )
| A. | 卫星的速度和角速度 | B. | 卫星的质量和轨道半径 | ||
| C. | 卫星的质量和角速度 | D. | 卫星的运行周期和轨道半径 |
