题目内容
17. 如图是用自由落体法验证机械能守恒定律时得到的一条纸带,有关尺寸已在图中注明,取n点来验证机械能守恒定律,下面列举一些计算n点速度的方法,其中正确的是( )
如图是用自由落体法验证机械能守恒定律时得到的一条纸带,有关尺寸已在图中注明,取n点来验证机械能守恒定律,下面列举一些计算n点速度的方法,其中正确的是( )| A. | n点是第n个点,则vn=gnT | B. | n点是第n个点,则vn=g(n-1)T | ||
| C. | vn=$\frac{{x}_{n}+{x}_{n+1}}{2T}$ | D. | vn=$\frac{{h}_{n+1}-{h}_{n-1}}{2T}$ |
分析 该实验是验证机械能守恒定律的实验,不能把重物看成自由落体运动,再运用自由落体的规律求解速度,那么就不需要验证了,求速度时我们是利用匀变速直线运动的规律即匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度.
解答 解:A、该实验是验证机械能守恒定律的实验,不能把重物看成自由落体运动,再运用自由落体的规律求解速度,那么就不需要验证了,AB选项都是利用了自由落体运动规律求速度的,故AB错误;
C、根据匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小可以求出某点的瞬时速度,由力可知,n-1到n+1之间的距离为xn+xn+1或hn+1-hn-1;
可以求出N点的速度为:vN=$\frac{{x}_{n}+{x}_{n+1}}{2T}$,或vN=$\frac{{h}_{n+1}-{h}_{n-1}}{2T}$,故AB错误,CD正确.
故选:CD.
点评 本题考查验证机械能守恒定律的数据分析方法,要注意明确实验原理,知道不能根据实验结论来验证结论,只能根据纸带来求解速度和重力势能的改变量.

练习册系列答案
相关题目
7.某同学为了测定某电源的电动势E和内阻r以及一段电阻丝的电阻率ρ,设计了如图(a)所示的电路.ab是一段电阻率较大的粗细均匀的电阻丝,R0是阻值为2Ω的保护电阻,滑动片P与电阻丝接触始终良好.实验时闭合电键,调节P的位置,将aP长度x和对应的电压U、电流I数据记录如下表:

(1)该同学根据实验数据绘制了如图(b)所示的U-I图象,可得电源的电动势E=3.0V;内阻 r=1Ω.
(2)请你根据表中数据在图(c)上描点连线作$\frac{U}{I}$和x关系图线.
(3)已知金属丝的横截面积s=0.12×10-6m2,利用图(c)图线,可以求得电阻丝的电阻率ρ为1.2×10-6Ω(保留两位有效数字);根据图(c)图线还可以得到的信息是电流表的内阻为2.0Ω.
| x(m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| U(V) | 1.50 | 1.72 | 1.95 | 2.00 | 2.10 | 2.18 |
| I(A) | 0.49 | 0.43 | 0.38 | 0.33 | 0.31 | 0.28 |
| U/I(Ω) | 3.06 | 4.00 | 5.13 | 6.06 | 6.77 | 7.79 |

(1)该同学根据实验数据绘制了如图(b)所示的U-I图象,可得电源的电动势E=3.0V;内阻 r=1Ω.
(2)请你根据表中数据在图(c)上描点连线作$\frac{U}{I}$和x关系图线.
(3)已知金属丝的横截面积s=0.12×10-6m2,利用图(c)图线,可以求得电阻丝的电阻率ρ为1.2×10-6Ω(保留两位有效数字);根据图(c)图线还可以得到的信息是电流表的内阻为2.0Ω.
5.放射性元素A经过2次α衰变和1次β衰变后生成一新元素B,则元素B在元素周期表中的位置较元素A的位置向前移动了( )
| A. | 1位 | B. | 2位 | C. | 3位 | D. | 4位 |
2.通过观察冥王星的卫星,可以推算出冥王星的质量.假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量.这两个物理量可以是( )
| A. | 卫星的速度和角速度 | B. | 卫星的质量和轨道半径 | ||
| C. | 卫星的质量和角速度 | D. | 卫星的运行周期和轨道半径 |
11. 图中A、B、C是三相交流电源的三根相线,O是中性线,电源的相电压为220V,L1、L2、L3是三个“220V 60W”的灯泡.开关S1断开,S2、S3闭合.由于某种原因,电源的中性线在图中O处断了,那么L2和L3两灯泡将( )
图中A、B、C是三相交流电源的三根相线,O是中性线,电源的相电压为220V,L1、L2、L3是三个“220V 60W”的灯泡.开关S1断开,S2、S3闭合.由于某种原因,电源的中性线在图中O处断了,那么L2和L3两灯泡将( )
 图中A、B、C是三相交流电源的三根相线,O是中性线,电源的相电压为220V,L1、L2、L3是三个“220V 60W”的灯泡.开关S1断开,S2、S3闭合.由于某种原因,电源的中性线在图中O处断了,那么L2和L3两灯泡将( )
图中A、B、C是三相交流电源的三根相线,O是中性线,电源的相电压为220V,L1、L2、L3是三个“220V 60W”的灯泡.开关S1断开,S2、S3闭合.由于某种原因,电源的中性线在图中O处断了,那么L2和L3两灯泡将( )| A. | 立刻熄灭 | B. | 变得比原来亮一些 | ||
| C. | 变得比原来暗一些 | D. | 保持亮度不变 |
12.某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.50cm,摆球直径为2.00cm,然后用秒表记录了单摆振动50次所用的时间为99.9s.如果他测得的g值偏小,可能的原因是( )
| A. | 测摆线长时摆线拉得过紧 | |
| B. | 实验中误将49次全振动数为50次 | |
| C. | 开始计时,秒表过迟按下 | |
| D. | 摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了 |
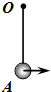 如图所示,一根长为L=0.2m的刚性轻绳,一端固定在O点,另一端连接一个质量为m的小球,当球自由悬挂时,球处在最低点A点,此时给球一个水平初速度v0让它运动起来,忽略空气阻力,重力加速度g=10m/s2
如图所示,一根长为L=0.2m的刚性轻绳,一端固定在O点,另一端连接一个质量为m的小球,当球自由悬挂时,球处在最低点A点,此时给球一个水平初速度v0让它运动起来,忽略空气阻力,重力加速度g=10m/s2 如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为L.在△OCA区域内有垂直于xOy平面向里的匀强磁场.质量为m、电荷量为q的带正电粒子,以平行于y轴的方向从OA边射入磁场.已知粒子从某点射入时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0.不计重力.
如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为L.在△OCA区域内有垂直于xOy平面向里的匀强磁场.质量为m、电荷量为q的带正电粒子,以平行于y轴的方向从OA边射入磁场.已知粒子从某点射入时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0.不计重力.