题目内容
20. 如图所示,有一半径为R的半圆形区域里存在垂直于圆面向外的匀强磁场(图中未画出),磁感应强度的大小为B,在圆心O处有一粒子源,可以沿垂直于磁场的不同方向向磁场中射入质量为m,电荷量为q、速度大小均为$\frac{qBR}{m}$的带正电的粒子(粒子重力不计),下列说法正确的是( )
如图所示,有一半径为R的半圆形区域里存在垂直于圆面向外的匀强磁场(图中未画出),磁感应强度的大小为B,在圆心O处有一粒子源,可以沿垂直于磁场的不同方向向磁场中射入质量为m,电荷量为q、速度大小均为$\frac{qBR}{m}$的带正电的粒子(粒子重力不计),下列说法正确的是( )| A. | 在半圆弧上各处都有粒子射出 | |
| B. | 粒子在磁场中运动的最长时间为$\frac{πm}{3qB}$ | |
| C. | 磁场中粒子不能达到的区域面积为$\frac{1}{12}$πR2 | |
| D. | 从半圆弧上射出的粒子在磁场中运动的时间相同 |
分析 粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,应用牛顿第二定律求出粒子的轨道半径,求出粒子在磁场中转过的圆心角,然后根据粒子周期公式分析答题.
解答 解:A、磁场垂直于纸面向外,粒子带正电,由左手定则可知,粒子在磁场中沿顺时针方向做匀速圆周运动,竖直向上射出的粒子运动轨迹如图所示,由几何知识可知:θ=60°,在该粒子轨迹与磁场边界交点上方无粒子射出,故A错误;
B、粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$, 已知:v=$\frac{qBR}{m}$,解得:r=R,故轨迹圆圆心、磁场区域圆圆心、出磁场的点构成等边三角形,故从半圆弧上射出的粒子在磁场中运动的轨迹对应的圆心角均为60°,粒子在磁场中转过的圆心角:α=θ=60°,粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,所有粒子在磁场中运动的时间相等,最长时间为:t=$\frac{α}{360°}$T=$\frac{πm}{3qB}$,故BD正确;
已知:v=$\frac{qBR}{m}$,解得:r=R,故轨迹圆圆心、磁场区域圆圆心、出磁场的点构成等边三角形,故从半圆弧上射出的粒子在磁场中运动的轨迹对应的圆心角均为60°,粒子在磁场中转过的圆心角:α=θ=60°,粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,所有粒子在磁场中运动的时间相等,最长时间为:t=$\frac{α}{360°}$T=$\frac{πm}{3qB}$,故BD正确;
C、粒子沿垂直于磁场的不同方向向磁场中射入,粒子能到达的区域如图中运动轨迹(红色)以下部分区域,粒子不能到达的区域面积:S=$\frac{\sqrt{3}}{4}$R2-$\frac{1}{12}$πR2,故C错误;
故选:BD.
点评 本题考查了粒子在磁场中的运动,粒子在磁场中做圆周运动,洛伦兹力提供向心力,分析清楚粒子运动过程、作出粒子运动轨迹是解题的关键,应用牛顿第二定律与粒子做圆周运动的周期公式可以解题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
10. 某运动员(可看做质点)参加跳台跳水比赛,其竖直方向的速度与时间关系图象如图所示,t=0是其向上起跳离开跳台瞬间,则( )
某运动员(可看做质点)参加跳台跳水比赛,其竖直方向的速度与时间关系图象如图所示,t=0是其向上起跳离开跳台瞬间,则( )
 某运动员(可看做质点)参加跳台跳水比赛,其竖直方向的速度与时间关系图象如图所示,t=0是其向上起跳离开跳台瞬间,则( )
某运动员(可看做质点)参加跳台跳水比赛,其竖直方向的速度与时间关系图象如图所示,t=0是其向上起跳离开跳台瞬间,则( )| A. | t1-t2时间内,运动员在水中正在下沉 | |
| B. | t2-t3时间内,运动员在水中正在上浮 | |
| C. | 由图象可知,运动员刚入水时的加速度最大 | |
| D. | 由图象可知,运动员在水中最深处时加速度为0 |
20. 如图所示,在圆形区域内有垂直于圆面向里的匀强磁场,磁感应强度为$\sqrt{3}$T,从磁场边缘A点,粒子源不断地沿各个方向向磁场中射入同一种粒子,粒子重力不计、速度相同,$\frac{1}{2}$圆弧上都有穿出磁场,若将穿出磁场的范围减为原来的$\frac{2}{3}$,若其他条件不变,则场强B′应变为( )
如图所示,在圆形区域内有垂直于圆面向里的匀强磁场,磁感应强度为$\sqrt{3}$T,从磁场边缘A点,粒子源不断地沿各个方向向磁场中射入同一种粒子,粒子重力不计、速度相同,$\frac{1}{2}$圆弧上都有穿出磁场,若将穿出磁场的范围减为原来的$\frac{2}{3}$,若其他条件不变,则场强B′应变为( )
 如图所示,在圆形区域内有垂直于圆面向里的匀强磁场,磁感应强度为$\sqrt{3}$T,从磁场边缘A点,粒子源不断地沿各个方向向磁场中射入同一种粒子,粒子重力不计、速度相同,$\frac{1}{2}$圆弧上都有穿出磁场,若将穿出磁场的范围减为原来的$\frac{2}{3}$,若其他条件不变,则场强B′应变为( )
如图所示,在圆形区域内有垂直于圆面向里的匀强磁场,磁感应强度为$\sqrt{3}$T,从磁场边缘A点,粒子源不断地沿各个方向向磁场中射入同一种粒子,粒子重力不计、速度相同,$\frac{1}{2}$圆弧上都有穿出磁场,若将穿出磁场的范围减为原来的$\frac{2}{3}$,若其他条件不变,则场强B′应变为( )| A. | 2$\sqrt{3}$T | B. | 2T | C. | $\frac{2\sqrt{3}}{3}$T | D. | 1.5T |
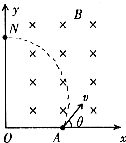 如图所示,有界匀强磁场的磁感应强度为B,区域足够大,方向垂直于纸面向里,直角坐标系xoy的y轴为磁场的左边界,A为固定在x轴上的一个放射源,内装镭核(${\;}_{88}^{226}$Ra)沿着与+x成θ=60°角方向释放一个α粒子后衰变成氡核(Rn),α粒子在y轴上的N点沿-x方向飞离磁场,N点到O点的距离为l,α粒子质量为m,电荷量为q,氡核的质量为M
如图所示,有界匀强磁场的磁感应强度为B,区域足够大,方向垂直于纸面向里,直角坐标系xoy的y轴为磁场的左边界,A为固定在x轴上的一个放射源,内装镭核(${\;}_{88}^{226}$Ra)沿着与+x成θ=60°角方向释放一个α粒子后衰变成氡核(Rn),α粒子在y轴上的N点沿-x方向飞离磁场,N点到O点的距离为l,α粒子质量为m,电荷量为q,氡核的质量为M 如图所示,一匝数N=10匝,边长L=20cm的正方形线圈在磁感应强度B=$\frac{2}{π}$T的匀强磁场中绕OO轴匀速转动,已知角速度ω=100πrad/s,线圈电阻忽略不计,外电阻R=20Ω.试问:
如图所示,一匝数N=10匝,边长L=20cm的正方形线圈在磁感应强度B=$\frac{2}{π}$T的匀强磁场中绕OO轴匀速转动,已知角速度ω=100πrad/s,线圈电阻忽略不计,外电阻R=20Ω.试问: 如图,手持一根长为L的轻绳的-端在水平桌面上做半径为r、角速度为ω匀速圆周运动,绳始终保持与该圆周相切,绳的另一端系一质量为m的小木块,木块也在桌面上做匀速圆周运动,不计空气阻力,求:
如图,手持一根长为L的轻绳的-端在水平桌面上做半径为r、角速度为ω匀速圆周运动,绳始终保持与该圆周相切,绳的另一端系一质量为m的小木块,木块也在桌面上做匀速圆周运动,不计空气阻力,求: 如图,与水平面成45°角的平面MN将空间分成Ⅰ和Ⅱ两个区域质量为m、电量为q的粒子以速度v0从平面MN上的P0点水平右射入I区.粒子在Ⅰ区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在Ⅱ区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里.粒子的重力可以忽略.求:
如图,与水平面成45°角的平面MN将空间分成Ⅰ和Ⅱ两个区域质量为m、电量为q的粒子以速度v0从平面MN上的P0点水平右射入I区.粒子在Ⅰ区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在Ⅱ区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里.粒子的重力可以忽略.求:
 如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度ω=2πrad/s,外电路电阻R=4Ω.求:(结论中可含有π)
如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度ω=2πrad/s,外电路电阻R=4Ω.求:(结论中可含有π)