题目内容
1. 竖直平面内有两个半径比为1:2的半圆形光滑轨道,如图所示.A、M、B三点位于同一水平面上,C、D分别为两轨道的最低点,将两个相同的小球分别从A、B处同时无初速释放( )
竖直平面内有两个半径比为1:2的半圆形光滑轨道,如图所示.A、M、B三点位于同一水平面上,C、D分别为两轨道的最低点,将两个相同的小球分别从A、B处同时无初速释放( )| A. | 通过C、D时,两球的线速度大小相等 | |
| B. | 到达C、D过程中,两球的重力做功相等 | |
| C. | 通过C、D时,两球的动能相等 | |
| D. | 通过C、D时,两球对轨道的压力相等 |
分析 根据机械能守恒定律分别求出两球通过C、D时的速度大小,从而分析动能的大小关系;根据重力做功的公式可求得重力所做的功;根据牛顿运动定律比较两球对轨道压力的大小.
解答 解:A、两球的初始位置机械能相等,下滑过程机械能都守恒,所以通过C、D时两球的机械能相等.设半圆轨道的半径为r,根据机械能守恒定律得:mgr=$\frac{1}{2}$mv2,解得:v=$\sqrt{2gr}$,则小球通过C点时的速度较小.故A错误;
B、重力做功W=mgh,因下落高度不同,故重力做功不相等,故B错误;
C、由A的分析可知,由于物体在C点速度较小,故小球在C点的动能较小,故C错误.
D、根据牛顿第二定律得:N-mg=ma$\frac{{v}^{2}}{r}$,代入A中求出的速度解得轨道对小球的支持力大小为N=3mg,则球对轨道的压力为N′=3mg,与质量无关,则通过C、D时,两球对轨道的压力相等.故D正确.
故选:D
点评 本题是机械能守恒定律与向心力知识的综合应用,小球通过最低点时的加速度、轨道的支持力与半径无关是经验结论,要在理解的基础上记住.

练习册系列答案
相关题目
12.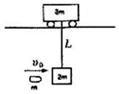 如图所示,质量为3m的小车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为2m的沙箱,一颗质量为m的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:沙箱上升到最高点时的速度.
如图所示,质量为3m的小车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为2m的沙箱,一颗质量为m的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:沙箱上升到最高点时的速度.
 如图所示,质量为3m的小车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为2m的沙箱,一颗质量为m的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:沙箱上升到最高点时的速度.
如图所示,质量为3m的小车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为2m的沙箱,一颗质量为m的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:沙箱上升到最高点时的速度.
9.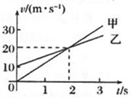 甲、乙两车在平直公路上同向行驶,其v-t图象如图所示.已知两车在t=2s时并排行驶,则( )
甲、乙两车在平直公路上同向行驶,其v-t图象如图所示.已知两车在t=2s时并排行驶,则( )
 甲、乙两车在平直公路上同向行驶,其v-t图象如图所示.已知两车在t=2s时并排行驶,则( )
甲、乙两车在平直公路上同向行驶,其v-t图象如图所示.已知两车在t=2s时并排行驶,则( )| A. | 甲车和乙车从同一地点出发 | B. | 在t=0时,甲车在乙车前10m | ||
| C. | 甲车的加速度小于乙车的加速度 | D. | 甲、乙车只相遇一次 |
16.下列说法不正确的是( )
| A. | 开普勒总结并提出了行星运动的三个定律 | |
| B. | 卡文迪许利用扭秤装置比较准确地测出了万有引力常量 | |
| C. | 伽利略认为“重的物体比轻物体下落得快” | |
| D. | 波兰天文学家哥白尼提出了“日心说”,大胆反驳“地心说” |
6.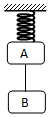 如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )
如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )
 如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )
如图,轻质弹簧下挂重为300N的物体A时伸长了3cm,再挂上重为200N的物体B时又伸长了2cm,现将AB间的细线烧断,使A在竖直平面内振动,则( )| A. | 最大回复力为300N,振幅为2cm | |
| B. | 最大回复力为200N,振幅为3cm | |
| C. | 只减小A的质量,振动的振幅变小,周期不变 | |
| D. | 只减小B的质量,振动的振幅变小,周期不变 |
3. 由光滑细管与光滑圆弧槽组成的轨道如图所示,其中AB段是圆弧槽,AB段和BC段都是半径为R的四分之一圆弧状,轨道固定在竖直平面内,一质量为m的小球,从距离水平地面高为H的管口D处由静止释放,最后能够从A端水平抛出落到地面上,下列说法正确的是( )
由光滑细管与光滑圆弧槽组成的轨道如图所示,其中AB段是圆弧槽,AB段和BC段都是半径为R的四分之一圆弧状,轨道固定在竖直平面内,一质量为m的小球,从距离水平地面高为H的管口D处由静止释放,最后能够从A端水平抛出落到地面上,下列说法正确的是( )
 由光滑细管与光滑圆弧槽组成的轨道如图所示,其中AB段是圆弧槽,AB段和BC段都是半径为R的四分之一圆弧状,轨道固定在竖直平面内,一质量为m的小球,从距离水平地面高为H的管口D处由静止释放,最后能够从A端水平抛出落到地面上,下列说法正确的是( )
由光滑细管与光滑圆弧槽组成的轨道如图所示,其中AB段是圆弧槽,AB段和BC段都是半径为R的四分之一圆弧状,轨道固定在竖直平面内,一质量为m的小球,从距离水平地面高为H的管口D处由静止释放,最后能够从A端水平抛出落到地面上,下列说法正确的是( )| A. | 小球释放的最小高度Hmin=$\frac{5}{2}$R | |
| B. | 小球释放的高度需满足H>2R | |
| C. | 小球落到地面时相对于A点的水平位移值至少为2R | |
| D. | 小球落到地面时相对于A点的水平位移值至少为2$\sqrt{2RH}$ |
1. 如图所示,某人在对面的山坡上水平抛出两个质量不等的小石块,分别落在A、B两处.不计空气阻力,则落到B处的石块( )
如图所示,某人在对面的山坡上水平抛出两个质量不等的小石块,分别落在A、B两处.不计空气阻力,则落到B处的石块( )
 如图所示,某人在对面的山坡上水平抛出两个质量不等的小石块,分别落在A、B两处.不计空气阻力,则落到B处的石块( )
如图所示,某人在对面的山坡上水平抛出两个质量不等的小石块,分别落在A、B两处.不计空气阻力,则落到B处的石块( )| A. | 初速度小,运动时间长 | B. | 初速度大,运动时间长 | ||
| C. | 初速度小,运动时间短 | D. | 初速度大,运动时间短 |
 如图所示是使用光电管的原理图,当用某种可见光照射到阴极K上时,电流表中有电流通过:
如图所示是使用光电管的原理图,当用某种可见光照射到阴极K上时,电流表中有电流通过: 如图所示,半径为R=0.75m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连线与水平方向间的夹角θ=37°,下端点C为轨道的最低点且与水平面相切.质量m=0.2kg的小物块 (可视为质点)从空中A点以v0=3m/s的速度被水平抛出,恰好从B点沿切线方向进入轨道,重力加速度取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,半径为R=0.75m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连线与水平方向间的夹角θ=37°,下端点C为轨道的最低点且与水平面相切.质量m=0.2kg的小物块 (可视为质点)从空中A点以v0=3m/s的速度被水平抛出,恰好从B点沿切线方向进入轨道,重力加速度取g=10m/s2,sin37°=0.6,cos37°=0.8.求: