题目内容
12.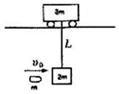 如图所示,质量为3m的小车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为2m的沙箱,一颗质量为m的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:沙箱上升到最高点时的速度.
如图所示,质量为3m的小车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为2m的沙箱,一颗质量为m的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求:沙箱上升到最高点时的速度.
分析 子弹打入沙箱过程中系统的动量守恒,根据动量守恒定律列式.沙箱向上摆动过程中,子弹、沙箱、小车系统水平方向动量守恒,机械能守恒.沙箱到达最大高度时系统有相同的速度,根据动量守恒定律和机械能守恒定律列式,联立方程即可求解.
解答 解:子弹打入沙箱过程中系统的动量守恒,取水平向右为正方向,根据动量守恒定律得:
mv0=(m+2m)v1 ①
沙箱向上摆动过程中,子弹、沙箱、小车系统水平方向动量守恒,系统的机械能也守恒.
沙箱到达最大高度时系统有相同的速度,设为v2,则有:
(m+2m)v1=(m+2m+3m)v2 ②
$\frac{1}{2}$(m+2m)v12=(m+2m)gh+$\frac{1}{2}$(m+2m+3m)v22③
联立①②③可得 h=$\frac{{v}_{0}^{2}}{36g}$
答:沙箱上升到最高点时的速度为$\frac{{v}_{0}^{2}}{36g}$.
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程,应用动量守恒定律与能量守恒定律即可正确解题,解题时要注意研究对象与运动过程的选择.

练习册系列答案
相关题目
20. 在物理学史上,利用如图所示的装置首先精确测引力常量的科学家是( )
在物理学史上,利用如图所示的装置首先精确测引力常量的科学家是( )
 在物理学史上,利用如图所示的装置首先精确测引力常量的科学家是( )
在物理学史上,利用如图所示的装置首先精确测引力常量的科学家是( )| A. | 爱因斯坦 | B. | 牛顿 | C. | 开普勒 | D. | 卡文迪许 |
7.有关光的本性,下列说法中正确的是( )
| A. | 光具有波动性,又具有粒子性,这是相互矛盾和对立的 | |
| B. | 光的干涉,衍射现象证明光具有粒子性,光电效应现象证明光具有波动性 | |
| C. | 大量光子才具有波动性,个别光子只具有粒子性 | |
| D. | 由于光既具有波动性,又具有粒子性,无法只用其中一种去说明光的一切现象,只能认为光具有波粒二象性 |
17. 如图所示,一物体由静止开始,从A点出发分别沿三个倾斜角不同但高度相同的粗糙斜面滑下,并分别从B、C、D三点滑至同一水平面上.三个斜面及水平面的动摩擦因数均相同,三个斜面并排放置,互不影响,斜面与水平面之间由很小一段曲面平滑连接,则( )
如图所示,一物体由静止开始,从A点出发分别沿三个倾斜角不同但高度相同的粗糙斜面滑下,并分别从B、C、D三点滑至同一水平面上.三个斜面及水平面的动摩擦因数均相同,三个斜面并排放置,互不影响,斜面与水平面之间由很小一段曲面平滑连接,则( )
 如图所示,一物体由静止开始,从A点出发分别沿三个倾斜角不同但高度相同的粗糙斜面滑下,并分别从B、C、D三点滑至同一水平面上.三个斜面及水平面的动摩擦因数均相同,三个斜面并排放置,互不影响,斜面与水平面之间由很小一段曲面平滑连接,则( )
如图所示,一物体由静止开始,从A点出发分别沿三个倾斜角不同但高度相同的粗糙斜面滑下,并分别从B、C、D三点滑至同一水平面上.三个斜面及水平面的动摩擦因数均相同,三个斜面并排放置,互不影响,斜面与水平面之间由很小一段曲面平滑连接,则( )| A. | 物体运动到B、C、D三点时,动能相等 | |
| B. | 物体运动到B、C、D三点时,重力的瞬时功率相等 | |
| C. | 物体在斜面上下滑的过程,其中沿AD斜面下滑重力的平均功率最大 | |
| D. | 物体从A点开始运动到最终停在水平面的过程中,全过程运动的水平距离相等 |
1. 竖直平面内有两个半径比为1:2的半圆形光滑轨道,如图所示.A、M、B三点位于同一水平面上,C、D分别为两轨道的最低点,将两个相同的小球分别从A、B处同时无初速释放( )
竖直平面内有两个半径比为1:2的半圆形光滑轨道,如图所示.A、M、B三点位于同一水平面上,C、D分别为两轨道的最低点,将两个相同的小球分别从A、B处同时无初速释放( )
 竖直平面内有两个半径比为1:2的半圆形光滑轨道,如图所示.A、M、B三点位于同一水平面上,C、D分别为两轨道的最低点,将两个相同的小球分别从A、B处同时无初速释放( )
竖直平面内有两个半径比为1:2的半圆形光滑轨道,如图所示.A、M、B三点位于同一水平面上,C、D分别为两轨道的最低点,将两个相同的小球分别从A、B处同时无初速释放( )| A. | 通过C、D时,两球的线速度大小相等 | |
| B. | 到达C、D过程中,两球的重力做功相等 | |
| C. | 通过C、D时,两球的动能相等 | |
| D. | 通过C、D时,两球对轨道的压力相等 |
12. 在河岸上,有人跨过定滑轮用长绳拴住一条小船,人以3m/s恒定的速率拉绳使小船靠岸,在小船靠岸过程中受到阻力作用.下列说法正确的是( )
在河岸上,有人跨过定滑轮用长绳拴住一条小船,人以3m/s恒定的速率拉绳使小船靠岸,在小船靠岸过程中受到阻力作用.下列说法正确的是( )
 在河岸上,有人跨过定滑轮用长绳拴住一条小船,人以3m/s恒定的速率拉绳使小船靠岸,在小船靠岸过程中受到阻力作用.下列说法正确的是( )
在河岸上,有人跨过定滑轮用长绳拴住一条小船,人以3m/s恒定的速率拉绳使小船靠岸,在小船靠岸过程中受到阻力作用.下列说法正确的是( )| A. | 如图位置时船速度大小为2$\sqrt{3}$m/s | B. | 小船靠岸过程做加速运动 | ||
| C. | 小船靠岸过程做减速运动 | D. | 小船动能的变化量等于拉力做的功 |
 如图所示,质量为m=1kg的物体,由竖直放置$\frac{1}{4}$的光滑圆弧轨道上端从静止开始下滑轨道静止不动,到达圆弧底端再沿水平面向右滑动一段距离而停止.已知圆弧轨道半径R=0.2m,圆弧轨道的上端与圆心在同一水平面内,g=10m/s2,μ=0.2,求:
如图所示,质量为m=1kg的物体,由竖直放置$\frac{1}{4}$的光滑圆弧轨道上端从静止开始下滑轨道静止不动,到达圆弧底端再沿水平面向右滑动一段距离而停止.已知圆弧轨道半径R=0.2m,圆弧轨道的上端与圆心在同一水平面内,g=10m/s2,μ=0.2,求: