题目内容
6. 如图所示电路,两根光滑金属导轨,平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计,斜面处在竖直向上的匀强磁场中,电阻可略去不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨匀速下滑,则它在下滑h高度的过程中,以下说法正确的是( )
如图所示电路,两根光滑金属导轨,平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计,斜面处在竖直向上的匀强磁场中,电阻可略去不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨匀速下滑,则它在下滑h高度的过程中,以下说法正确的是( )| A. | 作用在金属棒上各力的合力做功大于零 | |
| B. | 重力做功等于系统产生的电能 | |
| C. | 金属棒克服安培力做功等于电阻R上产生的焦耳热 | |
| D. | 金属棒克服恒力F做功等于电阻R上产生的焦耳热 |
分析 导体棒ab匀速下滑,合力为零,即可合力的做功为零;对导体棒正确受力分析,根据动能定理列方程,弄清功能转化关系,来分析功与能的关系.注意克服安培力所做功等于回路电阻中产生的焦耳热.
解答 解:A、导体棒匀速下滑的过程中,作用于棒上各力的合力为零,则合力所作的功等于零,故A错误.
B、根据动能定理得:WG-WF-W安=0,得WG=WF+W安,可知,重力做功等于金属棒克服安培力做的功与克服恒力F做的功之和,则重力做功大于金属棒克服安培力做的功,而金属棒克服安培力做功等于系统产生的电能,所以重力做功大于系统产生的电能.故B错误.
C、根据功能关系知,金属棒克服安培力做功等于电阻R上产生的焦耳热,故C正确.
D、电阻R上发出的焦耳热等于金属棒克服安培力做功,与金属棒克服恒力F做功无关,故D错误.
故选:C
点评 对于电磁感应与功能结合问题,要结合导体棒的运动状态,利用动能定理进行判断各个力做功之间关系,尤其注意的是克服安培力所做功等于整个回路中产生的电能.

练习册系列答案
相关题目
1.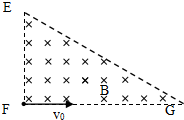 如图所示,匀强磁场的边界为直角三角形,∠EGF=30°,已知磁感应强度为B,方向垂直纸面向里.F处有一粒子源,沿FG方向发射出大量带正电荷q的同种粒子,粒子质量为m,粒子的初速度v0大小可调,则下列说法正确的是( )
如图所示,匀强磁场的边界为直角三角形,∠EGF=30°,已知磁感应强度为B,方向垂直纸面向里.F处有一粒子源,沿FG方向发射出大量带正电荷q的同种粒子,粒子质量为m,粒子的初速度v0大小可调,则下列说法正确的是( )
 如图所示,匀强磁场的边界为直角三角形,∠EGF=30°,已知磁感应强度为B,方向垂直纸面向里.F处有一粒子源,沿FG方向发射出大量带正电荷q的同种粒子,粒子质量为m,粒子的初速度v0大小可调,则下列说法正确的是( )
如图所示,匀强磁场的边界为直角三角形,∠EGF=30°,已知磁感应强度为B,方向垂直纸面向里.F处有一粒子源,沿FG方向发射出大量带正电荷q的同种粒子,粒子质量为m,粒子的初速度v0大小可调,则下列说法正确的是( )| A. | 若粒子能到达EG边界,则粒子速度越大,从F运动到EG边的时间越长 | |
| B. | v0取合适值,粒子可以到达E点 | |
| C. | 能到达EF边界的所有粒子所用的时间均相等 | |
| D. | 粒子从F运动到EG边所用的最长时间为$\frac{5πm}{12qB}$ |
18.对于电动势和内电阻确定的电源的路端电压,下列说法正确的是(I、U、R分别表示干路电流、路端电压和外电阻)( )
| A. | U随R的增大而减小 | B. | 当R=0时,U=0 | ||
| C. | 当电路断开时,I=0,U=E | D. | 当R增大时,U也会增大 |
15.一检验电荷q=+3×10-9C,在电场中P点受到的电场力F=6×10-7N,P点的电场强度为2×102N/C;若将检验电荷电荷量变为q′=+2×10-8C 放在P点,受的电场力为4×10-6N.
16.某物理实验小组用下列器材进行实验,描绘一种特殊元件的伏安特性曲线,所测数据记录在表格中:
器材:A.待测元件Rx
B.电流表A(0~50mA,内阻约为200Ω)
C.电压表V1(0~3V,内阻约为10kΩ)
D.电压表V2(0~6V,内阻约为15kΩ)
E.滑动变阻器R1(0~20Ω,2A)
F.滑动变阻器R2(0~200Ω,0.2A)
G.学生电源(直流4V)
H.开关及导线
(1)为了调节方便,尽可能准确测量,电压表应选C,滑动变阻器应选E.(填器材前面的序号)
(2)从如图1的几个电路图中,选出合适的实验电路图C.

(3)在坐标纸上用描点法画出元件的伏安特性(I~U)曲线,如图2所示.
(4)若该元件的最佳工作电压为2.8V,现用电动势为4V,内阻r=5Ω的电源为其供电,则要在电路中串联一个阻值为R=35Ω的电阻,才能使其处于最佳工作状态.
器材:A.待测元件Rx
B.电流表A(0~50mA,内阻约为200Ω)
C.电压表V1(0~3V,内阻约为10kΩ)
D.电压表V2(0~6V,内阻约为15kΩ)
E.滑动变阻器R1(0~20Ω,2A)
F.滑动变阻器R2(0~200Ω,0.2A)
G.学生电源(直流4V)
H.开关及导线
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| U/V | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 | 2.6 | 2.8 | 3.0 |
| I/mA | 0 | 0.9 | 2.2 | 4.2 | 6.7 | 11.9 | 19.0 | 23.8 | 30.0 | 37.1 |
(2)从如图1的几个电路图中,选出合适的实验电路图C.

(3)在坐标纸上用描点法画出元件的伏安特性(I~U)曲线,如图2所示.
(4)若该元件的最佳工作电压为2.8V,现用电动势为4V,内阻r=5Ω的电源为其供电,则要在电路中串联一个阻值为R=35Ω的电阻,才能使其处于最佳工作状态.
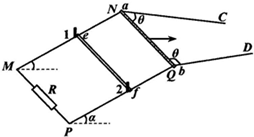 如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ.均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g.
如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ.均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g.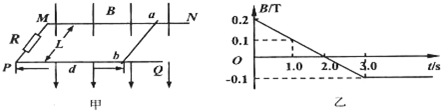
 如图所示.质量为m=2kg的物块,带电量q=1.0×10-3c,从区域左边界的A点以v0=5m/s的初速度进入AB区域.在水平面上运动.物块与水平面之间的摩擦系数为μ=0.4,AB区域的宽度L=1.25m.(上下宽度足够宽)并在AB区域内有方向水平向右的匀强电场,大小为E=4.0×103,(图中未画出)轨道的半圆部分光滑,半径R=40cm,求:
如图所示.质量为m=2kg的物块,带电量q=1.0×10-3c,从区域左边界的A点以v0=5m/s的初速度进入AB区域.在水平面上运动.物块与水平面之间的摩擦系数为μ=0.4,AB区域的宽度L=1.25m.(上下宽度足够宽)并在AB区域内有方向水平向右的匀强电场,大小为E=4.0×103,(图中未画出)轨道的半圆部分光滑,半径R=40cm,求: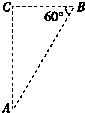 如图所示,A、B、C三点都在匀强电场中.已知AC⊥BC,∠ABC=60°,BC=20cm.把一个q=10-5 C的正电荷从A移到B,电场力做功为零;从B移到C,电场力做功为-1.73×10-3 J,则该匀强电场的场强大小是1000V/m,并在图中作出过C点电场线和等势面.
如图所示,A、B、C三点都在匀强电场中.已知AC⊥BC,∠ABC=60°,BC=20cm.把一个q=10-5 C的正电荷从A移到B,电场力做功为零;从B移到C,电场力做功为-1.73×10-3 J,则该匀强电场的场强大小是1000V/m,并在图中作出过C点电场线和等势面.