题目内容
14. 如图所示.质量为m=2kg的物块,带电量q=1.0×10-3c,从区域左边界的A点以v0=5m/s的初速度进入AB区域.在水平面上运动.物块与水平面之间的摩擦系数为μ=0.4,AB区域的宽度L=1.25m.(上下宽度足够宽)并在AB区域内有方向水平向右的匀强电场,大小为E=4.0×103,(图中未画出)轨道的半圆部分光滑,半径R=40cm,求:
如图所示.质量为m=2kg的物块,带电量q=1.0×10-3c,从区域左边界的A点以v0=5m/s的初速度进入AB区域.在水平面上运动.物块与水平面之间的摩擦系数为μ=0.4,AB区域的宽度L=1.25m.(上下宽度足够宽)并在AB区域内有方向水平向右的匀强电场,大小为E=4.0×103,(图中未画出)轨道的半圆部分光滑,半径R=40cm,求:(1)物块通过AB区域过程中电场力做的功
(2)物块运动到轨道最高点C点时对轨道的压力
(3)物块从C点飞出后落到水平面上的位置距C点的水平距离;
(4)若电场强度的大小不变方向变为竖直向下,物块滑到区域右边界时的动能.
分析 (1)根据功的公式W=FS即可求出电场力的功;
(2)A到C的过程中电场力、摩擦力和重力做功,由动能定理即可求出C点的速度,然后结合牛顿第二定律求出C对轨道的压力;
(3)物块离开C后做平抛运动,将小球的运动分解即可求出;
(4)若电场强度的大小不变方向变为竖直向下,摩擦力对物块做功,由动能定理即可求出物块滑到区域右边界时的动能.
解答  解:(1)电场力做功为:W=qEL=1.0×10-3×4.0×103×1.25=5 J
解:(1)电场力做功为:W=qEL=1.0×10-3×4.0×103×1.25=5 J
(2)物块从A到C由动能定理得:
$W-μmgL-mg•2R=\frac{1}{2}m{v}_{C}^{2}-\frac{1}{2}m{v}_{0}^{2}$
代入数据解得:vc=2 m/s
物块在C点:${F}_{N}+mg=\frac{m{v}_{c}^{2}}{R}$
代入数据解得:FN=0
即物块对轨道压力为零
(3)物块从C点抛出后下落时间:t=$\sqrt{\frac{2×2R}{g}}=\sqrt{\frac{2×2×0.4}{10}}=0.4$s
若物块从C点抛出后下落过程中始终在AB区域内运动,水平方向:
$a=\frac{qE}{m}=\frac{1.0×1{0}^{-3}×4.0×1{0}^{3}}{2}=2m/{s}^{2}$
因此,水平方向的位移:$x={v}_{c}t-\frac{1}{2}a{t}^{2}$
代入数据得:x=0.64m
(4)当电场强度方向向下后运动到右边界时动能为Ek
则:${E}_{k}-\frac{1}{2}m{v}_{0}^{2}=-μ(mg+qE)$
代入数据解得:Ek=15.4J
答:(1)物块通过AB区域过程中电场力做的功是5J;
(2)物块运动到轨道最高点C点时对轨道的压力是0;
(3)物块从C点飞出后落到水平面上的位置距C点的水平距离是0.64m;
(4)若电场强度的大小不变方向变为竖直向下,物块滑到区域右边界时的动能是15.4J.
点评 该题结合电场力考查竖直平面内的圆周运动与平抛运动,涉及的知识点多,物体的受力、运动过程多,在解答的过程中首先要把握各过程中的受力,然后选择合适的公式进行解答.

 如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )| A. | a粒子的速度比b粒子速度小 | |
| B. | a粒子在磁场中的运动时间比b粒子短 | |
| C. | 两粒子离开磁场时的速度反向延长线一定都过圆心 | |
| D. | 两粒子离开磁场时的速度反向延长线不一定都过圆心 |
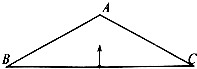 顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )
顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )| A. | 1:3 | B. | 1:2 | C. | (2$\sqrt{3}-3$):1 | D. | 1:1 |
 如图所示电路,两根光滑金属导轨,平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计,斜面处在竖直向上的匀强磁场中,电阻可略去不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨匀速下滑,则它在下滑h高度的过程中,以下说法正确的是( )
如图所示电路,两根光滑金属导轨,平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计,斜面处在竖直向上的匀强磁场中,电阻可略去不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨匀速下滑,则它在下滑h高度的过程中,以下说法正确的是( )| A. | 作用在金属棒上各力的合力做功大于零 | |
| B. | 重力做功等于系统产生的电能 | |
| C. | 金属棒克服安培力做功等于电阻R上产生的焦耳热 | |
| D. | 金属棒克服恒力F做功等于电阻R上产生的焦耳热 |
| A. | 电场线并非真实存在,是假想出来的,既能反映电场的强弱,也能反映电场的方向 | |
| B. | 电场线处处与等势面垂直 | |
| C. | 只要初速度为零,正电荷必将沿电场线方向移动 | |
| D. | 负电荷所受电场力方向一定与电场线切线方向相反 |
| A. | 桌面受到了向下的弹力,是由于桌面发生形变而产生的 | |
| B. | 书本受到了向下的弹力,是由于桌面发生形变而产生的 | |
| C. | 书本受到了向上的弹力,是由于桌面发生形变而产生的 | |
| D. | 桌面受到了向上的弹力,是由于书本发生形变而产生的 |
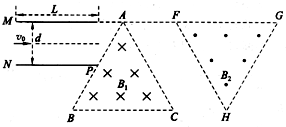
 如图所示,在xOy平面内存在I、II、III、IV四个场区,y轴右侧存在匀强磁场I,y轴左侧与虚线MN之间存在方向相反的两个匀强电场,II区电场方向竖直向下,III区电场方向竖直向上,P点是MN与x轴的交点.有一质量为m,带电荷量+q的带电粒子由原点O,以速度v0沿x轴正方向水平射入磁场I,已知匀强磁场I的磁感应强度垂直纸面向里,大小为2B0,匀强电场II和匀强电场III的电场强度大小均为E=$\frac{{{B_0}{v_0}}}{2}$,如图所示,IV区的磁场垂直纸面向外,大小为B0,OP之间的距离为$\frac{{4m{v_0}}}{{q{B_0}}}$,已知粒子最后能回到O点.
如图所示,在xOy平面内存在I、II、III、IV四个场区,y轴右侧存在匀强磁场I,y轴左侧与虚线MN之间存在方向相反的两个匀强电场,II区电场方向竖直向下,III区电场方向竖直向上,P点是MN与x轴的交点.有一质量为m,带电荷量+q的带电粒子由原点O,以速度v0沿x轴正方向水平射入磁场I,已知匀强磁场I的磁感应强度垂直纸面向里,大小为2B0,匀强电场II和匀强电场III的电场强度大小均为E=$\frac{{{B_0}{v_0}}}{2}$,如图所示,IV区的磁场垂直纸面向外,大小为B0,OP之间的距离为$\frac{{4m{v_0}}}{{q{B_0}}}$,已知粒子最后能回到O点. 如图所示,平行金属板长为L,一个带电为+q质量为m的粒子以初速度v0紧贴上板垂直射入电场,刚好从下板边缘射出,末速度恰与下板成30°角,粒子重力不计,求:
如图所示,平行金属板长为L,一个带电为+q质量为m的粒子以初速度v0紧贴上板垂直射入电场,刚好从下板边缘射出,末速度恰与下板成30°角,粒子重力不计,求: