题目内容
17. 一个倾角θ=37°的光滑斜面,用一条平行于斜面的细绳拴住一个质量m=2kg的小球,如图所示,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.
一个倾角θ=37°的光滑斜面,用一条平行于斜面的细绳拴住一个质量m=2kg的小球,如图所示,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.(1)若此光滑斜面静止在地面上,小球所受的支持力,拉力分别多大?
(2)若此光滑斜面在向左做匀加速运动,问加速度多大时斜面对球的支持力为零?
(3)如果加速度等于10$\sqrt{3}$m/s2,拉力是多大?
分析 (1)对小球受力分析,将重力分解为沿着斜面和垂直于斜面,再根据平衡条件求出支持力和拉力;
(2)对小球受力分析,抓住竖直方向上合力为零,水平方向上有合力,合力方向水平向左,结合牛顿定律求出加速度的大小;
(3)当加速度等于10$\sqrt{3}$m/s2,先判断小球是否飘离斜面,再分别水平和竖直方向分析,求出拉力;
解答  解:(1)对小球受力分析,如图所示,受到竖直向下的重力mg,沿着斜面向上的绳子拉力T
解:(1)对小球受力分析,如图所示,受到竖直向下的重力mg,沿着斜面向上的绳子拉力T
斜面对小球的支持力N
若此光滑斜面静止在地面上,则小球受到的支持力大小等于重力在垂直于斜面的分力
即N=G2=mgcosθ=2×10×cos37°=16N
小球受到的拉力T大小等于重力沿着斜面向下的分力
即T=G1=mgsinθ=2×10×sin37°=12N
(2)若此光滑斜面在向左做匀加速运动,设加速度为a时,斜面对球的支持力为零
则此时竖直方向:Tsinθ=mg
水平方向:Tcosθ=ma
解得a=$\frac{40}{3}m/{s}^{2}$
(3)如果加速度等于10$\sqrt{3}$m/s2,因为加速度大于$\frac{40}{3}m/{s}^{2}$,则此时小球已经飘离斜面
设此时拉力T与水平方向的夹角为α
则此时竖直方向:Tsinα=mg
水平方向:Tcosθ=ma′
解得:T=20N;
答:(1)若此光滑斜面静止在地面上,小球所受的支持力大小为16N,拉力大小为12N;
(2)若此光滑斜面在向左做匀加速运动,加速度为$\frac{40}{3}m/{s}^{2}$时斜面对球的支持力为零;
(3)如果加速度等于10$\sqrt{3}$m/s2,拉力大小为20N.
点评 解决本题的关键是能够正确地受力分析,运用正交分解,根据牛顿第二定律进行求解,第(3)问比较容易出错,误以为拉力与水平方向夹角还是37°,要先判断小球是否已经飘离斜面.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案 如图所示是某卫星绕地球飞行的三条轨道,其中轨道1是近地圆形轨道,轨道2和3是变轨后的椭圆轨道,它们相切于A点.卫星在轨道1上运行时经过A点的速率为v,加速度大小为a,下列说法正确的是( )
如图所示是某卫星绕地球飞行的三条轨道,其中轨道1是近地圆形轨道,轨道2和3是变轨后的椭圆轨道,它们相切于A点.卫星在轨道1上运行时经过A点的速率为v,加速度大小为a,下列说法正确的是( )| A. | 卫星在轨道2上经过A点时的速率大于v | |
| B. | 卫星在轨道2上经过A点时的加速度大于a | |
| C. | 卫星在轨道2上运行的周期大于在轨道3上运行的周期 | |
| D. | 卫星在轨道2上具有的机械能大于在轨道3上具有的机械能 |

| A. | Gcosα | B. | Gtanα | C. | G | D. | Gsinα |
 某兴趣小组利用如图a所示实验装置测重力加速度.倾斜的球槽中放有若干个小铁球,闭合开关K,电磁铁吸住第1个小球.手动敲击弹性金属片M,M与触头瞬间分开,第1个小球开始下落,M迅速恢复,电磁铁又吸住第2个小球.当第1个小球撞击M 时,M与触头分开,第2个小球开始下落….这样,就可测出n个小球下落的总时间T.
某兴趣小组利用如图a所示实验装置测重力加速度.倾斜的球槽中放有若干个小铁球,闭合开关K,电磁铁吸住第1个小球.手动敲击弹性金属片M,M与触头瞬间分开,第1个小球开始下落,M迅速恢复,电磁铁又吸住第2个小球.当第1个小球撞击M 时,M与触头分开,第2个小球开始下落….这样,就可测出n个小球下落的总时间T.
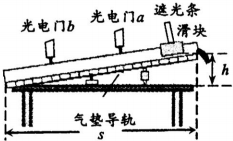 某同学用图示装置验证机械能守恒定律.先将气垫导轨倾斜放置,用刻度尺分别测出固定在导轨上的两个光电门a、b中心之间的距离L、导轨两端的水平距离s、两端的高度差h;接着利用游标卡尺测出滑块上遮光条的宽度d.
某同学用图示装置验证机械能守恒定律.先将气垫导轨倾斜放置,用刻度尺分别测出固定在导轨上的两个光电门a、b中心之间的距离L、导轨两端的水平距离s、两端的高度差h;接着利用游标卡尺测出滑块上遮光条的宽度d. ”型板框,将一质量为m的带电小球用绝缘细杆悬挂在框中.杆与竖直线成30°夹角.现使整体在匀强磁场B中沿垂直于磁场
”型板框,将一质量为m的带电小球用绝缘细杆悬挂在框中.杆与竖直线成30°夹角.现使整体在匀强磁场B中沿垂直于磁场
 同.实验室提供的器材有:
同.实验室提供的器材有: